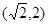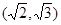题目内容
已知圆x2+y2=1和直线y=2x+b相交于A,B两点,且OA,OB是x轴正方向沿逆时针分别旋转α,β角而得,则cos(α+β)的值为( )
A.
| B.
| ||||||
C.
| D.
|
由
消去y得:5x2+4bx+b2-1=0,
设A(x1,y1),B(x2,y2),
则x1、x2是方程5x2+4bx+b2-1=0的两根,
∴由韦达定理得:x1+x2=-
,x1x2=
,
∴y1y2=(2x1+b)(2x2+b)
=4x1x2+2b(x1+x2)+b2
=
-
b2+b2
=
,
又cosα=x1,cosβ=x2,sinα=y1,sinβ=y2,
∴cos(α+β)=cosαcosβ-sinαsinβ
=x1x2-y1y2
=
-
=
.
故选:B.
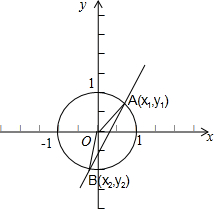
|
设A(x1,y1),B(x2,y2),
则x1、x2是方程5x2+4bx+b2-1=0的两根,
∴由韦达定理得:x1+x2=-
| 4b |
| 5 |
| b2-1 |
| 5 |
∴y1y2=(2x1+b)(2x2+b)
=4x1x2+2b(x1+x2)+b2
=
| 4(b2-1) |
| 5 |
| 8 |
| 5 |
=
| b2-4 |
| 5 |
又cosα=x1,cosβ=x2,sinα=y1,sinβ=y2,
∴cos(α+β)=cosαcosβ-sinαsinβ
=x1x2-y1y2
=
| b2-1 |
| 5 |
| b2-4 |
| 5 |
=
| 3 |
| 5 |
故选:B.
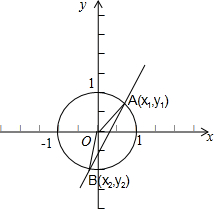

练习册系列答案
相关题目
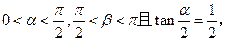
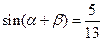 .
.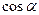 与
与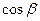 的值;(2)求
的值;(2)求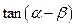 的值.
的值.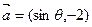 与
与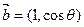 互相垂直,其中
互相垂直,其中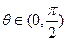 .
.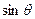 和
和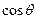 的值;
的值;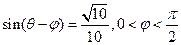 ,求
,求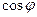 的值.
的值. 的范围是( )
的范围是( )