题目内容
已知函数f(x)=sin(x-
)+
cos(x-
).
(Ⅰ)求函数y=f(x)-1的单调递增区间;
(Ⅱ)设函数g(x)=(1+sinx)f(x),求g(x)的值域.
| π |
| 3 |
| 3 |
| π |
| 3 |
(Ⅰ)求函数y=f(x)-1的单调递增区间;
(Ⅱ)设函数g(x)=(1+sinx)f(x),求g(x)的值域.
(Ⅰ)函数f(x)=sin(x-
)+
cos(x-
)=2sin[x-
)+
]=2sinx,…(3分)
∵y=sinx的单调增区间为[2kπ-
2kπ+
],k∈z,
∴y=f(x)-1的单调增区间是[2kπ-
,2kπ+
]k∈Z.…(6分)
(Ⅱ)由(Ⅰ)可得,函数g(x)=(1+sinx)f(x)=2sin2x+2sinx.…(7分)
设 t=sinx,当x∈R时,t∈[-1,1],则h(t)=2t2+2t=2(t+
)2-
.…(9分)
由二次函数的单调性可知,h(t)的最小值为 h(-
)=-
,最大值为h(1)=4,…(11分)
则函数h(t)的值域为[-
,4],故g(x)的值域为[-
,4].…(12分)
| π |
| 3 |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∵y=sinx的单调增区间为[2kπ-
| π |
| 2 |
| π |
| 2 |
∴y=f(x)-1的单调增区间是[2kπ-
| π |
| 2 |
| π |
| 2 |
(Ⅱ)由(Ⅰ)可得,函数g(x)=(1+sinx)f(x)=2sin2x+2sinx.…(7分)
设 t=sinx,当x∈R时,t∈[-1,1],则h(t)=2t2+2t=2(t+
| 1 |
| 2 |
| 1 |
| 2 |
由二次函数的单调性可知,h(t)的最小值为 h(-
| 1 |
| 2 |
| 1 |
| 2 |
则函数h(t)的值域为[-
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目
 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为 ,且满足
,且满足
 ,求
,求 .
.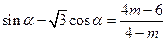 有意义,则应有( )
有意义,则应有( )