题目内容
设函数
（1）若
，求曲线
在
处的切线方程；
（2）若
恒成立，求
的取值范围。
（1）
；（2）
解析试题分析：（1）根据题意，由于函数，则可知
当，切线在点（0，0）的斜率为4，那么可知曲线在处的切线方程为；
（2）对于要使得恒成立，则可知只要求解函数的最小值大于等于零即可，那么根据，函数为偶函数，只要证明
的最小值即可。那么求解导数大于零或者小于零的不等式可知函数单调性，得到的取值范围；
考点：导数、不等式
点评：本题考查导数、不等式、函数的单调性、最值等知识，考查化归与转化、分类与讨论的数学思想方法，属难题．
练习册系列答案
金博士一点全通系列答案
相关题目
石恒成立，求实数a的取值范围，
，
为
的导函数.
，求
的值；
图象与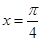
对称，△ABC的三个内角A、B、C所对的边长分别为
，角A为
，求△ABC面积的最大值.
时，求
的极小值；
对任意的
都不是曲线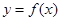
的切线，求
的取值范围；
，求
的最大值
的解析式．
上是减函数的充要条件；
图象上的点
处的切线方程；
，其中
是自然对数的底数，
，
恒成立，求实数
的取值范围。
的大小关系；
和
是否存在公切线，若存在，求出公切线方程，若不存在，说明理由；
的大小，并写出判断过程．
在x=1处与直线
相切．
，
的值；②求函数
在
上的最大值.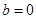
时，若不等式
对所有的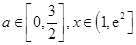
都成立，求实数
的取值范围.
在点
处的切线与直线
平行，求出这条切线的方程；
，讨论函数
的单调区间；
，恒有
，求实数
的取值范围.