题目内容
已知函数f (x) = 
(1)试判断当 的大小关系;
的大小关系;
(2)试判断曲线 和
和 是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;
是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;
(3)试比较 (1 + 1×2) (1 + 2×3) ……(1 +2012×2013)与 的大小,并写出判断过程.
的大小,并写出判断过程.
(1)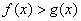 ;
;
(2)方程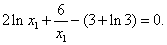 无解,故二者没有公切线。
无解,故二者没有公切线。
(3) (1 + 1×2) (1 + 2×3) ……(1 +2012×2013) 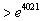 。
。
解析试题分析:(1)设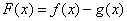 ,则
,则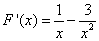 1分
1分
由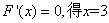 ,
,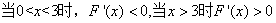
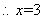 时, 2分
时, 2分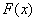 在区间
在区间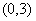 单调递减,在区间
单调递减,在区间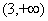 单调递增, 3分
单调递增, 3分
所以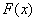 取得最小值为
取得最小值为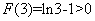 ,
,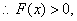 即
即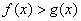 4分
4分
(2)假设曲线 有公切线,切点分别为
有公切线,切点分别为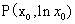 和
和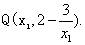 5分
5分
因为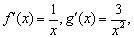 ,所以分别以
,所以分别以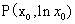 和
和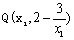 为切线的切线方程为
为切线的切线方程为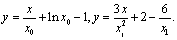 6分
6分
令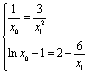 即
即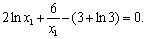 8分
8分
令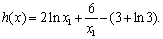 所以由
所以由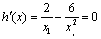 得
得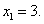 显然,当
显然,当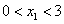 时,
时,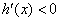 ,当
,当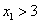 时,
时,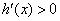 ,所以
,所以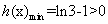 , 9分
, 9分
所以方程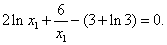 无解,故二者没有公切线。 10分
无解,故二者没有公切线。 10分
(3)由(1)得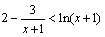 对任意的x>0都成立,
对任意的x>0都成立,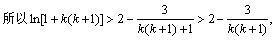 11分
11分
ln(1 + 1×2) + ln(1 + 2×3) + …+ln[1 + n (n + 1)]>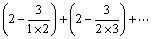
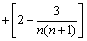 =
=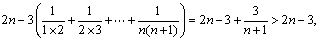 令
令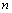 =2012, 13分
=2012, 13分
则ln(1 + 1×2) + ln(1 + 2×3) + …+ln(1 + 2012×2013) >2×2012-3=4021,
所以(1 + 1×2) (1 + 2×3) ……(1 +2012×2013) 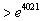 14分
14分
考点:本题主要考查导数的几何意义,直线方程,应用导数研究函数的单调性、最值及不等式恒成立问题。
点评:典型题,本题属于导数应用中的基本问题,通过研究函数的单调性,明确了极值情况。涉及比较大小问题,通过构造函数,转化成了研究函数的单调性及最值。涉及对数函数,要特别注意函数的定义域。

 期末集结号系列答案
期末集结号系列答案

 恒成立?若存在,求出a的取值条件;
恒成立?若存在,求出a的取值条件;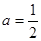 时,求证:f(1)+f(2)+f(3)+…+
时,求证:f(1)+f(2)+f(3)+…+ .
. 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间 上是减函数,又
上是减函数,又 .
. 的解析式;
的解析式; (m>0)上恒有
(m>0)上恒有
 ,求曲线
,求曲线 在
在 处的切线方程;
处的切线方程; 恒成立,求
恒成立,求 的取值范围。
的取值范围。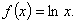
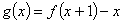 的最大值;
的最大值;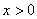 ,不等式
,不等式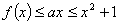 恒成立,求实数
恒成立,求实数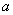 的取值范围;
的取值范围;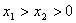 ,求证:
,求证: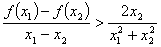 .
. ,
, ,求函数
,求函数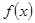 的极小值,
的极小值, ,设
,设 ,函数
,函数 .若存在
.若存在 使得
使得 成立,求
成立,求 的取值范围.
的取值范围.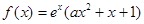 ,
,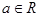 ;
; 的单调性;
的单调性; 上的最大值为
上的最大值为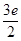 ,求
,求 的值.
的值. .(
.( )
) 时,试确定函数
时,试确定函数 在其定义域内的单调性;
在其定义域内的单调性; 上的最小值;
上的最小值; .
.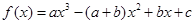 其中
其中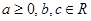
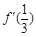 =0,求
=0,求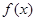 的单调区间;
的单调区间;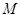 表示
表示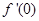 与
与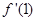 两个数中的最大值,求证:当0≤x≤1时,|
两个数中的最大值,求证:当0≤x≤1时,|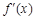 |≤
|≤