题目内容
已知f(x)=1nx-a(x-l),a∈R
(I)讨论f(x)的单调性;
(Ⅱ)若x≥1时, 石恒成立,求实数a的取值范围,
石恒成立,求实数a的取值范围,
(I) 在
在 上单调递增;在
上单调递增;在 上单调递减.(Ⅱ)
上单调递减.(Ⅱ)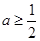
解析试题分析:解:(Ⅰ) 的定义域为
的定义域为 ,
, .
.
①当 时,则
时,则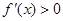 ,∴
,∴ 在
在 上单调递增;
上单调递增;
②当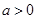 时,令
时,令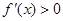 ,得
,得 ;令
;令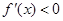 ,得
,得 ,
,
∴ 在
在 上单调递增;在
上单调递增;在 上单调递减.
上单调递减.
(Ⅱ)由题意,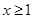 时,
时, 恒成立.
恒成立.
设 ,则
,则 对
对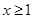 时恒成立.
时恒成立.
则
①当 时,
时, ,即
,即 在
在 上单调递减,
上单调递减,
∴当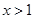 时,
时, 与
与 恒成立矛盾.
恒成立矛盾.
②当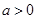 时,对于方程
时,对于方程 (*),
(*),
(ⅰ)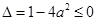 ,即
,即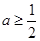 时,
时, ,即
,即 在
在 上单调递增,
上单调递增,
∴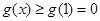 符合题意.
符合题意.
(ⅱ)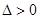 ,即
,即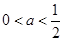 时,方程(*)有两个不等实根
时,方程(*)有两个不等实根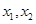 ,不妨设
,不妨设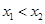 ,则
,则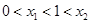 ,
,
当 时,
时, ,即
,即 递减,∴
递减,∴ 与
与 恒成立矛盾.
恒成立矛盾.
综上,实数 的取值范围为
的取值范围为 .
.
另解: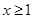 时,
时, 恒成立,
恒成立,
当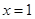 时,上式显然成立;当
时,上式显然成立;当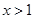 时,
时, 恒成立.
恒成立.
设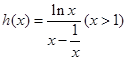 ,可证
,可证 在
在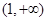 上单调递减(需证明),
上单调递减(需证明),
又由洛必达法则知,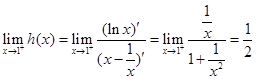 ,∴
,∴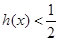 .
.
故,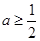 .
.
考点:导数的应用
点评:导数常应用于求曲线的切线方程、求函数的最值与单调区间、证明不等式和解不等式中参数的取值范围等。

练习册系列答案
相关题目
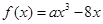 与
与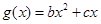 的图像都过点
的图像都过点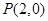 ,且它们在点
,且它们在点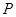 处有公共切线.
处有公共切线. 和
和 的表达式及在点
的表达式及在点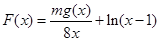 ,其中
,其中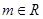 ,求
,求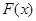 的单调区间.
的单调区间.
 在
在 上的最大值和最小值.
上的最大值和最小值. 作曲线
作曲线 的切线,求此切线的方程.
的切线,求此切线的方程. 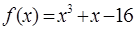 .
. 在点
在点 处的切线方程;
处的切线方程; 为曲线
为曲线 的切线,且经过原点,求直线
的切线,且经过原点,求直线 的方程及切点坐标
的方程及切点坐标 ,
,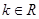 .
.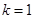 ,求函数
,求函数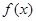 的单调区间;
的单调区间;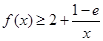 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,若对任意的两个实数
,若对任意的两个实数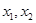 满足
满足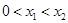 ,总存在
,总存在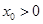 ,使得
,使得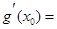
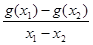 成立,证明:
成立,证明: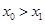 .
. .
. 奇偶性, 并求出函数
奇偶性, 并求出函数 的单调区间;
的单调区间;  有零点,求实数
有零点,求实数 的取值范围.
的取值范围.

 恒成立?若存在,求出a的取值条件;
恒成立?若存在,求出a的取值条件;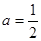 时,求证:f(1)+f(2)+f(3)+…+
时,求证:f(1)+f(2)+f(3)+…+ .
.
 ,判断函数在定义域内的单调性;
,判断函数在定义域内的单调性; 内存在极值,求实数m的取值范围。
内存在极值,求实数m的取值范围。
 ,求曲线
,求曲线 在
在 处的切线方程;
处的切线方程; 恒成立,求
恒成立,求 的取值范围。
的取值范围。