题目内容
1.已知数量{an}满足:a1=$\frac{1}{3}$,an+1=an+$\frac{{a}_{n}^{2}}{{n}^{2}}$(n∈N*).(1)证明:对一切n∈N*有an<an+1;
(2)证明:$\frac{4n-1}{9n}$<an<$\frac{n-1}{n}$(n≥2).
分析 (1)通过an+1=an+$\frac{{a}_{n}^{2}}{{n}^{2}}$(n∈N*),可知an+1-an=$\frac{{a}_{n}^{2}}{{n}^{2}}$>0,进而可得结论;
(2)一方面通过(1)、放缩可知an+1<an+$\frac{1}{{n}^{2}}$•anan+1,将等式两边同时除以anan+1可知$\frac{1}{{a}_{n}}$<$\frac{1}{{a}_{n+1}}$+$\frac{1}{{n}^{2}}$,通过累加、放缩可知当n≥2时$\frac{1}{{a}_{n}}$>$\frac{n}{n-1}$即an<$\frac{n-1}{n}$;另一方面通过a1=$\frac{1}{3}$、an+1=an+$\frac{{a}_{n}^{2}}{{n}^{2}}$可知a2=$\frac{4}{9}$,从而当n≥2时an≥$\frac{4}{9}$>$\frac{4n-1}{9n}$.
解答 证明:(1)∵an+1=an+$\frac{{a}_{n}^{2}}{{n}^{2}}$(n∈N*),
∴an+1-an=$\frac{{a}_{n}^{2}}{{n}^{2}}$>0,
又∵a1=$\frac{1}{3}$>0,
∴对一切n∈N*有0<an<an+1;
(2)由(1)可知,an+1=an+$\frac{{a}_{n}^{2}}{{n}^{2}}$<an+$\frac{1}{{n}^{2}}$•anan+1,
∴$\frac{1}{{a}_{n}}$<$\frac{1}{{a}_{n+1}}$+$\frac{1}{{n}^{2}}$,
∴当n≥2时,$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{1}}$-$\sum_{k=1}^{n-1}$($\frac{1}{{a}_{k}}$-$\frac{1}{{a}_{k+1}}$)
>$\frac{1}{{a}_{1}}$-$\sum_{k=1}^{n-1}$$\frac{1}{{k}^{2}}$
>3-[1+$\sum_{k=1}^{n-1}$$\frac{1}{k(k-1)}$]
=3-[1+$\sum_{k=1}^{n-1}$($\frac{1}{k-1}$-$\frac{1}{k}$)]
=3-(1+1-$\frac{1}{n-1}$)
=$\frac{n}{n-1}$,
∴an<$\frac{n-1}{n}$;
另一方面,由a1=$\frac{1}{3}$、an+1=an+$\frac{{a}_{n}^{2}}{{n}^{2}}$可知a2=a1+${{a}_{1}}^{2}$=$\frac{1}{3}+\frac{1}{{3}^{2}}$=$\frac{4}{9}$,
∴an≥a2=$\frac{4}{9}$>$\frac{4n-1}{9n}$(n≥2);
综上所述,$\frac{4n-1}{9n}$<an<$\frac{n-1}{n}$(n≥2).
点评 本题是一道关于数列与不等式的综合题,注意解题方法的积累,属于中档题.

| A. | A=0,B≠0 | B. | A≠0,B=0 | C. | A=0,B≠0,C≠0 | D. | A≠0,B=0,C≠0 |
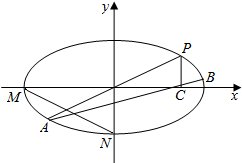 如图,在平面直角坐标系xOy中,M、N分别是椭圆$\frac{x^2}{4}+\frac{y^2}{2}=1$的顶点,过坐标原点的直线交椭圆于P,A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C,设直线PA的斜率为k.
如图,在平面直角坐标系xOy中,M、N分别是椭圆$\frac{x^2}{4}+\frac{y^2}{2}=1$的顶点,过坐标原点的直线交椭圆于P,A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C,设直线PA的斜率为k.