题目内容
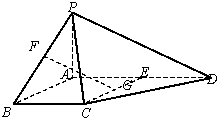
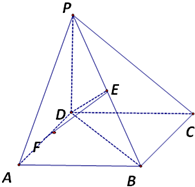
如图，四棱锥P-ABCD的底面ABCD是正方形，PA⊥底面ABCD，E，F分别是AC，PB的中点．
（Ⅰ）证明：EF∥平面PCD；
（Ⅱ）若PA=AB，求EF与平面PAC所成角的大小．
（Ⅰ）证明：EF∥平面PCD；
（Ⅱ）若PA=AB，求EF与平面PAC所成角的大小．
（Ⅰ）证明：如图，连接BD，则E是BD的中点．
又F是PB的中点，
所以EF∥PD．
因为EF不在平面PCD内，
所以EF∥平面PCD．（6分）
（Ⅱ）连接PE．
因为ABCD是正方形，
所以BD⊥AC．
又PA⊥平面ABC，
所以PA⊥BD．
因此BD⊥平面PAC．
故∠EPD是PD与平面PAC所成的角．
因为EF∥PD，
所以EF与平面PAC所成的角的大小等于∠EPD．
因为PA=AB=AD，∠PAD=∠BAD=90°，
所以Rt△PAD≌Rt△BAD．
因此PD=BD．
在Rt△PED中，
sin∠EPD=
=
，
∠EPD=30°．
所以EF与平面PAC所成角的大小是30°．（14分）
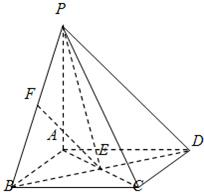
又F是PB的中点，
所以EF∥PD．
因为EF不在平面PCD内，
所以EF∥平面PCD．（6分）
（Ⅱ）连接PE．
因为ABCD是正方形，
所以BD⊥AC．
又PA⊥平面ABC，
所以PA⊥BD．
因此BD⊥平面PAC．
故∠EPD是PD与平面PAC所成的角．
因为EF∥PD，
所以EF与平面PAC所成的角的大小等于∠EPD．
因为PA=AB=AD，∠PAD=∠BAD=90°，
所以Rt△PAD≌Rt△BAD．
因此PD=BD．
在Rt△PED中，
sin∠EPD=
| ED |
| PD |
| 1 |
| 2 |
∠EPD=30°．
所以EF与平面PAC所成角的大小是30°．（14分）
练习册系列答案
相关题目
