题目内容
17. 已知两点F1(-1,0),F2(1,0),点P在以F1,F2为焦点的椭圆C,且|PF1|,|F1F2|,|PF2|构成等差数列.
已知两点F1(-1,0),F2(1,0),点P在以F1,F2为焦点的椭圆C,且|PF1|,|F1F2|,|PF2|构成等差数列.(1)求椭圆C的方程;
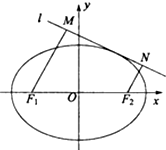
(2)如图,动直线l:y=kx+m(|k|≤1)(m>0)与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且F1M⊥l,F2N⊥l,当|F1M|+|F2N|最大时,求直线l的方程.
分析 (1)依题意,设椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,c=1.再利用|PF1|、|F1F2|、|PF2|构成等差数列,即可得到a,利用b2=a2-c2得到a即可得到椭圆的方程;
(2)将直线l的方程y=kx+m代入椭圆C的方程3x2+4y2=12中,得到关于x的一元二次方程,由直线l与椭圆C仅有一个公共点知,△=0,即可得到m,k的关系式,利用点到直线的距离公式即可得到|F1M|+|F2N|,利用|F1M|+|F2N|最大时,即可求直线l的方程.
解答 解:(Ⅰ)依题意,设椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0).
∵|PF1|、|F1F2|、|PF2|构成等差数列,
∴2a=|PF1|+|PF2|=2|F1F2|=4,a=2.
又∵c=1,∴b2=3.∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$…(4分)
(Ⅱ)将直线l的方程y=kx+m代入椭圆C的方程中,得
(4k2+3)x2+8kmx+4m2-12=0.
由直线l与椭圆C仅有一个公共点知,△=64k2m2-4(4k2+3)(4m2-12)=0,
化简得:m2=4k2+3. …(6分)
设坐标原点到动直线L的距离为d,则
2d=|F1M|+|F2N|=2$\sqrt{\frac{{m}^{2}}{1+{k}^{2}}}$…(8分)
=2$\sqrt{4-\frac{1}{1+{k}^{2}}}$,
∵k2≤1,∴k2=1时,|F1M|+|F2N|最大
此时m=$\sqrt{7}$.
故所求直线方程为y=-x+$\sqrt{7}$或y=x+$\sqrt{7}$…(12分)
点评 本题主要考查椭圆的方程与性质、直线方程、直线与椭圆的位置关系、等差数列等基础知识,考查运算能力、推理论证以及分析问题、解决问题的能力,考查数形结合、化归与转化思想.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案| A. | x1<x2<x3<x4 | B. | x3<x1<x4<x2 | C. | x1<x3<x4<x2 | D. | x1<x3<x2<x4 |
| A. | p真q真 | B. | p真q假 | C. | p假q假 | D. | p假q真 |