题目内容
19.已知椭圆C的中心在坐标原点O,右焦点F($\sqrt{3}$,0),M、N是椭圆C的左、右顶点,D是椭圆C上异于M、N的动点,且△MND面积的最大值为2.(Ⅰ)求椭圆C的方程;
(Ⅱ)设斜率为$\frac{1}{2}$的直线,与椭圆C相交于A,B两点,求△OAB的面积的最大值,并写出此时直线l的方程.
分析 (Ⅰ)设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由题意可得a2-b2=3,当D为椭圆的上(或下)顶点,△MND的面积最大,且为ab=2,解方程可得a,b,进而得到椭圆方程;
(Ⅱ)由于直线的斜率为k=$\frac{1}{2}$,可设直线l:y=$\frac{1}{2}$x+m,代入椭圆方程,消去y,运用韦达定理和判别式大于0,再由弦长公式和点到直线的距离公式,结合基本不等式,可得三角形的面积的最大值,即可得到所求直线的方程.
解答 解:(Ⅰ)设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由题意可得c=$\sqrt{3}$,即a2-b2=3,
当D为椭圆的上(或下)顶点,△MND的面积最大,
且为ab=2,
解得a=2,b=1,
即有椭圆的方程为$\frac{{x}^{2}}{4}$+y2=1;
(Ⅱ)由于直线的斜率为k=$\frac{1}{2}$,可设直线l:y=$\frac{1}{2}$x+m,
代入椭圆方程可得,x2+2mx+2m2-2=0,
则x1+x2=-2m,x1x2=2m2-2,
由判别式△=(-2m)2-4(2m2-2)>0,解得m2<2,
由|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{5}$•$\sqrt{2-{m}^{2}}$,
O到直线AB的距离为d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$=$\frac{2|m|}{\sqrt{5}}$,
即有S△OAB=$\frac{1}{2}$|AB|•d=|m|•$\sqrt{2-{m}^{2}}$≤$\frac{{m}^{2}+(2-{m}^{2})}{2}$=1,
当且仅当|m|=$\sqrt{2-{m}^{2}}$,即为m=±1取得等号.
则△OAB的面积的最大值为1,此时直线l的方程为y=$\frac{1}{2}$x+1,或y=$\frac{1}{2}$x-1.
点评 本题考查椭圆的方程和性质,同时考查直线和椭圆方程联立,运用韦达定理和弦长公式,考查基本不等式的运用:求最值,属于中档题.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案| A. | 通过分析残差有利于发现样本数据中的可疑数据 | |
| B. | 根据获取的样本数据计算${\sum_{i=1}^n{({{y_i}-\overline y})}^2}$,若${\sum_{i=1}^n{({{y_i}-\overline y})}^2}$越小,则模型的拟合效果越好 | |
| C. | 根据获取的样本数据计算$\sum_{i=1}^n{{{({{y_i}-\hat y})}^2}}$,若$\sum_{i=1}^n{{{({{y_i}-\hat y})}^2}}$越大,则模型的拟合效果越差 | |
| D. | 根据获取的样本数据计算R2,若R2=0.85,则表明解释变量解释了85%的预报变量变化 |
| A. | p∨q真 | B. | p∧q真 | C. | ¬p真 | D. | ¬q假 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{3π}{4}$ | B. | $\frac{π}{4}$ | C. | 0 | D. | -$\frac{π}{4}$ |
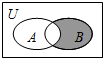 设全集U是实数集R,集合A={y|y=3x,x>0},B={x|y=$\sqrt{2x-{x}^{2}}$},则图中阴影部分所表示的集合是( )
设全集U是实数集R,集合A={y|y=3x,x>0},B={x|y=$\sqrt{2x-{x}^{2}}$},则图中阴影部分所表示的集合是( )| A. | {x|0≤x<1} | B. | {x|0≤x≤1} | C. | {x|1<x<2} | D. | {x|1<x≤2} |