题目内容
【题目】已知函数![]() ,其图象的一条切线为
,其图象的一条切线为![]() .
.
(1)求实数![]() 的值;
的值;
(2)求证:若![]() ,则
,则![]() .
.
【答案】(1)![]() ;(2)答案见解析
;(2)答案见解析
【解析】
(1)假设切点,根据曲线在某点处导数的几何意义,以及已知的切线方程,可得![]() ,然后研究
,然后研究![]() 可得
可得![]() ,最后代值计算,可得结果.
,最后代值计算,可得结果.
(2)构建函数![]() ,计算
,计算![]() ,并利用二阶导判断
,并利用二阶导判断![]() 的单调性,根据
的单调性,根据![]() 的值域来判断
的值域来判断![]() 的单调性,进一步求得
的单调性,进一步求得![]() ,可得结果.
,可得结果.
(1)函数定义域为![]()
∵![]() ,∴
,∴![]() .
.
由题可知:
![]() 在点
在点![]() 处的切线为
处的切线为![]() ,
,
则![]() 且
且![]() ,
,
∴![]() ,即
,即![]() .
.
令![]() ,
,
则![]() .
.
当![]() 时,
时,
![]() ,
,![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,
时,
![]() ,
,![]() 在
在![]() 单调递减.
单调递减.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
∴![]() ,
,![]() .故实数
.故实数![]() 的值为
的值为![]() .
.
(2)令![]()
即![]()
则![]() .
.
即![]()
令![]() ,
,
则![]() ,
,
∵![]() 恒成立,
恒成立,
∴![]() 在
在![]() 单调递减,即
单调递减,即![]() 在
在![]() 单调递减.
单调递减.
又![]() ,
,
![]() ,
,
∴![]() ,使得
,使得![]() .
.
∴当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
故![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
∴![]() .
.
又![]() ,即
,即![]() ,
,
∴![]() ,
,
![]()
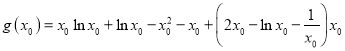
![]() .
.
令![]() ,
,![]() .
.
则![]() .
.
∵![]() 恒成立,
恒成立,
∴![]() ,故
,故![]() 在
在![]() 单调递增.
单调递增.
∴![]() ,
,
故![]() ,
,
即![]() .
.
∴当![]() 时,
时,![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目