题目内容
已知函数f(x)为偶函数,满足f(x+1)=1-f(x),当x∈[0,1]时,f(x)=x,若在区间[-1,3]内,函数g(x)=f(x)-kx-k有四个零点,则实数k的取值范围是______.
由f(x+1)=1-f(x)可得函数f(x+2)=1-f(x+1)=1-[1-f(x)]=f(x),故函数f(x)是以2为周期的周期函数.
函数g(x)=f(x)-kx-k有四个零点,故函数y=f(x)的图象与直线y=k(x+1)在区间[-1,3]内有4个交点.
再根据函数f(x)为偶函数,如图所示:可得0<k,且 k(3+1)≤1,求得0<k≤
,
故答案为 (0,
].
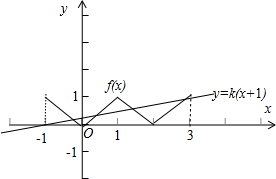
函数g(x)=f(x)-kx-k有四个零点,故函数y=f(x)的图象与直线y=k(x+1)在区间[-1,3]内有4个交点.
再根据函数f(x)为偶函数,如图所示:可得0<k,且 k(3+1)≤1,求得0<k≤
| 1 |
| 4 |
故答案为 (0,
| 1 |
| 4 |


练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
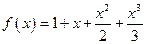 的零点的个数是 ( )
的零点的个数是 ( )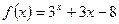 ,用二分法求方程
,用二分法求方程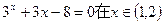 内近似解的过程中得
内近似解的过程中得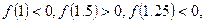 则方程的根落在区间
则方程的根落在区间 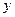 表示成
表示成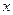 的函数,并写出该函数的定义域.
的函数,并写出该函数的定义域.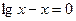 根的个数为( )
根的个数为( )