题目内容
对于直角坐标平面内的任意两点 、
、 ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”:
‖AB‖= ,给出下列三个命题:
,给出下列三个命题:
①若点C在线段AB上,则‖AC‖+‖CB‖=‖AB‖;
②在△ABC中,若∠C=90°,则‖AC‖+‖CB‖=‖AB‖;
③在△ABC中,‖AC‖+‖CB‖>‖AB‖.
其中真命题的个数为
| A.0 | B.1 | C.2 | D.3 |
B
解析试题分析:解:对于直角坐标平面内的任意两点A(x1,y1),B(x2,y2),定义它们之间的一种“距离”:|AB|=|x2-x1|+|y2-y1|.对于①若点C在线段AB上,设C点坐标为(x0,y0),x0在x1、x2之间,y0在y1、y2之间,则|AC|+|CB|=|x0-x1|+|y0-y1|+|x2-x0|+|y2-y0|=|x2-x1|+|y2-y1|=|AB|成立,故①正确.对于②平方后不能消除x0,y0,命题不成立;对于③在△ABC中,|AC|+|CB|=|x0-x1|+|y0-y1|+|x2-x0|+|y2-y0|≥|(x0-x1)+(x2-x0)|+|(y0-y1)+(y2-y0)|=|x2-x1|+|y2-y1|=|AB|.③不一定成立∴命题①成立,故选:B.
考点:新定义的应用
点评:此题主要考查新定义的问题,对于此类型的题目需要认真分析题目的定义再求解,切记不可脱离题目要求.属于中档题目.本题的易错点在于不等式:|a|+|b|≥|a+b|忘记等号也可以成立

练习册系列答案
相关题目
命题 对
对 ,都有
,都有 成立,则
成立,则 的否定形式为( )
的否定形式为( )
A.对 ,都有 ,都有 | B. ,都有 ,都有 |
C. ,都有 ,都有 | D.对 ,都有 ,都有 |
“x>1”是“ >x”的( )
>x”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列有关命题的说法正确的是( )
A.命题“若 ,则 ,则 ”的否命题为“若 ”的否命题为“若 ,则 ,则 ” ” |
B.命题“ ”的否定是“ ”的否定是“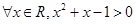 ” ” |
C.命题“若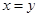 ,则 ,则 ”的逆否命题为假命题 ”的逆否命题为假命题 |
| D.若“p或q”为真命题,则p,q至少有一个为真命题 |
设 ,则
,则 是
是
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题“若A∩B=A,则A B的逆否命题是( )
B的逆否命题是( )
A.若A∪B≠A,则A B B | B.若A∩B≠A,则A B B |
C.若A B,则A∩B≠A B,则A∩B≠A | D.若A B,则A∩B≠A B,则A∩B≠A |
设甲:函数 的值域为
的值域为 ,乙:函数
,乙:函数 有四个单调区间,那么甲是乙的( )
有四个单调区间,那么甲是乙的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
若 ,
, 是非零向量,“
是非零向量,“ ⊥
⊥ ”是“函数
”是“函数 为一次函数”的( )
为一次函数”的( )
| A.充分而不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |