题目内容
3.(1)用“五点法”作函数$y=2sin(\frac{x}{2}+\frac{π}{3}),x∈R$的简图;(2)该函数的图象可由函数y=sinx,x∈R的图象经过怎样的变换得出?
分析 (1)根据“五点法”即可画出函数在长度为一个周期的闭区间上的简图;
(2)根据三角函数图象之间的关系,即可得到结论.
解答 解(1):①列表:
| $\frac{1}{2}x$+$\frac{π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{2π}{3}$ | $\frac{π}{3}$ | $\frac{4π}{3}$ | $\frac{7π}{3}$ | $\frac{10π}{3}$ |
| y | 0 | 2 | 0 | -2 | 0 |
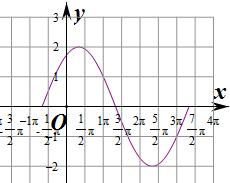
③用光滑的曲线连接这五点,得所要求作的函数图象.
(2)①把y=sinx,x∈R的图象向左平移$\frac{π}{3}$个单位,所得图象
对应的析式为y=sin(x+$\frac{π}{3}$).
②再把y=sin(x+$\frac{π}{3}$)的图象纵坐标不变,横坐标伸长为原来的2倍,所得图象
对应的解析式为y=sin($\frac{1}{2}$x+$\frac{π}{3}$).
③再把y=sin($\frac{1}{2}$x+$\frac{π}{3}$)的图象横坐标不变,纵坐标伸长为原来的2倍,所得图象的
解析式为y=2sin($\frac{1}{2}$x+$\frac{π}{3}$).
点评 本题主要考查三角函数的图象和性质,要求熟练掌握五点法作图以及函数图象之间的变化关系.

练习册系列答案
相关题目
11.由集合{a1},{a1,a2},{a1,a2,a3},…的子集个数归纳出集合{a1,a2,a3,…,an}的子集个数为 ( )
| A. | n | B. | n+1 | C. | 2n | D. | 2n-1 |