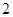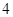题目内容
如图,点A、B为椭圆
+
=1长轴的两个端点,点M为该椭圆上位于第一象限内的任意一点,直线AM、BM分别与直线l:x=2
相交于点P、Q.
(1)若点P、Q关于x轴对称,求点M的坐标;
(2)证明:椭圆右焦点F在以线段PQ为直径的圆上.

| x2 |
| 4 |
| y2 |
| 2 |
| 2 |
(1)若点P、Q关于x轴对称,求点M的坐标;
(2)证明:椭圆右焦点F在以线段PQ为直径的圆上.

(1)由题意,a=2,∴A(2,0),B(-2,0).
设点M的坐标为(x0,y0),则直线AM的方程为y=
(x-2),
令x=2
,则P(2
,
•(2
-2)).
同理,Q((2
,
•(2
+2)).
∵点P、Q关于x轴对称,
∴
•(2
-2)+
•(2
+2)=0,
∴x0=
,
代入椭圆方程,
∵点M为该椭圆上位于第一象限内的任意一点,
∴y0=1,
∴点M的坐标为(
,1);
(2)证明:∵c=
=
,
∴F(
,0),
∴
•
=2+
•
(2
-2)(2
+2)=
,
∵
+
=1,
∴x02+2y02=0,
∴
•
=0,
∴
⊥
,
∴FP⊥FQ,
∴椭圆右焦点F在以线段PQ为直径的圆上.
设点M的坐标为(x0,y0),则直线AM的方程为y=
| y0 |
| x0-2 |
令x=2
| 2 |
| 2 |
| y0 |
| x0-2 |
| 2 |
同理,Q((2
| 2 |
| y0 |
| x0+2 |
| 2 |
∵点P、Q关于x轴对称,
∴
| y0 |
| x0-2 |
| 2 |
| y0 |
| x0+2 |
| 2 |
∴x0=
| 2 |
代入椭圆方程,
∵点M为该椭圆上位于第一象限内的任意一点,
∴y0=1,
∴点M的坐标为(
| 2 |
(2)证明:∵c=
| 4-2 |
| 2 |
∴F(
| 2 |
∴
| FP |
| FQ |
| y0 |
| x0-2 |
| y0 |
| x0+2 |
| 2 |
| 2 |
| 2(x02+2y02-4) |
| x02-4 |
∵
| x02 |
| 4 |
| y02 |
| 2 |
∴x02+2y02=0,
∴
| FP |
| FQ |
∴
| FP |
| FQ |
∴FP⊥FQ,
∴椭圆右焦点F在以线段PQ为直径的圆上.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
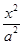 -
-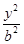 =1(a>0,b>0)的左、右焦点分别为F1、F2,过点F2作与x轴垂直的直线与双曲线一个交点为P,且∠PF1F2=
=1(a>0,b>0)的左、右焦点分别为F1、F2,过点F2作与x轴垂直的直线与双曲线一个交点为P,且∠PF1F2=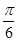 ,则双曲线的渐近线方程为________.
,则双曲线的渐近线方程为________.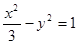 的焦距为( ).
的焦距为( ).