题目内容
已知三条直线l1:2x-y+a =" 0" (a>0),直线l2:-4x+2y+1 = 0和直线l3:x+y-1= 0,且l1与l2的距离是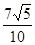 .
.
(1)求a的值;
(2)能否找到一点P,使得P点同时满足下列三个条 件:
①P是第一象限的点;
②P 点到l1的距离是P点到l2的距离的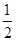 ;
;
③P点到l1的距离与P点到l3的距离之比是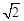 ∶
∶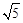 .若能,求P点坐标;若不能,说明理由.
.若能,求P点坐标;若不能,说明理由.
(1)a = 3;(2)P(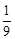 ,
,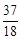 )
)
解析试题分析:(1)将两直线方程化为同系数方程,利用两直线间距离公式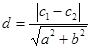 计算得a = 3;(2)设点P(x0,y0),若P点满足条件②,则P点在与l1、l2平行的直线
计算得a = 3;(2)设点P(x0,y0),若P点满足条件②,则P点在与l1、l2平行的直线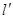 :2x-y+c =" 0" 上,由平行线间的距离公式得
:2x-y+c =" 0" 上,由平行线间的距离公式得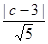 =
= ×
×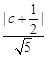 ,所以c =
,所以c =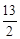 或c =
或c =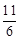 ,即2x0-y0+
,即2x0-y0+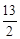 = 0或2x0-y0+
= 0或2x0-y0+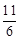 = 0,若P点满足条件③由点到直线的距离公式有x0-2y0+4= 0或3x0+2 = 0,又结合条件①解得
= 0,若P点满足条件③由点到直线的距离公式有x0-2y0+4= 0或3x0+2 = 0,又结合条件①解得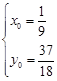 ,即点P(
,即点P(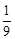 ,
,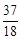 )为能同时满足三个条件的点.
)为能同时满足三个条件的点.
试题解析:(1)l2方程变形为2x-y- = 0,
= 0,
∴l1与l2的距离d =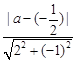 =
=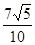

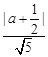 =
=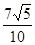 ,
,
∴|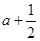 | =
| =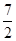 ,由a>0解得a = 3.
,由a>0解得a = 3.
(2)设点P(x0,y0),若P点满足条件②,则P点在与l1、l2平行的直线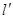 :2x-y+c =" 0" 上.
:2x-y+c =" 0" 上.
且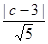 =
= ×
×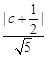 ,解得c =
,解得c =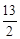 或c =
或c =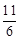 ,∴2x0-y0+
,∴2x0-y0+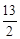 = 0或2x0-y0+
= 0或2x0-y0+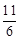 = 0;
= 0;
若P点满足条件③,由点到直线的距离公式,有 =
=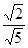 ·
·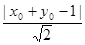 ,即|
,即|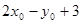 | = |
| = | |,
|,
∴x0-2y0+4= 0或3x0+2 = 0;
由P在第一象限,显然3x0+2 = 0不可能,
联立方程2x0-y0+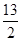 = 0和x0-2y0+4= 0,解得
= 0和x0-2y0+4= 0,解得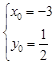 (舍去),
(舍去),
联立方程2x0-y0+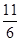 = 0和x0-2y0+4= 0,解得
= 0和x0-2y0+4= 0,解得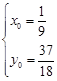 ,
,
∴点P(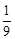 ,
,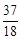 )即为能同时满足三个条件的点.
)即为能同时满足三个条件的点.
考点:直线的方程与位置关系及距离公式的应用

 阅读快车系列答案
阅读快车系列答案 经过直线
经过直线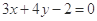 与直线
与直线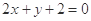 的交点
的交点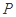 ,且垂直于直线
,且垂直于直线 .(1)求直线
.(1)求直线 .
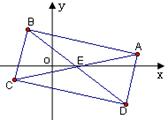
.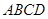 的两条对角线的交点为
的两条对角线的交点为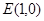 ,且
,且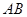 与
与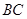 所在的直线方程分别为
所在的直线方程分别为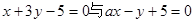 .
.
 所在的直线方程;
所在的直线方程; 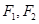 分别为椭圆
分别为椭圆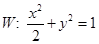 的左、右焦点,斜率为
的左、右焦点,斜率为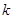 的直线
的直线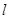 经过右焦点
经过右焦点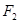 ,且与椭圆W相交于
,且与椭圆W相交于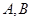 两点.
两点. 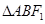 的周长;
的周长; 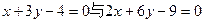 的距离是 .
的距离是 .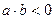 时,如果直线
时,如果直线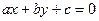 的倾斜角
的倾斜角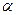 满足关系式
满足关系式 ,则此直线方程的斜率为 ;
,则此直线方程的斜率为 ; 与
与 垂直,则
垂直,则 ______.
______.