题目内容
已知直线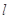 经过直线
经过直线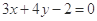 与直线
与直线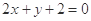 的交点
的交点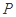 ,且垂直于直线
,且垂直于直线 .(1)求直线
.(1)求直线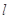 的方程;(2)求直线
的方程;(2)求直线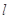 与两坐标轴围成的三角形的面积
与两坐标轴围成的三角形的面积 .
.
(1)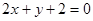 ;(2)1.
;(2)1.
解析试题分析:(1)法一:先联立两已知直线方程,求出两直线的交点坐标,再由垂直的关系求出直线的斜率,最后由点斜式就可写出所求直线的方程;法二:先由过两直线交点的直线系方程,再由互相垂直二直线的斜率之积等于-1,就可求出其中参数值,从而获得所求直线方程;只是要注意直线系方程的形式;
(2)由(1)的结果不难求得直线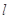 与两坐标轴的交点坐标,并知直线
与两坐标轴的交点坐标,并知直线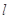 与两坐标轴围成的三角形是直角三角形,故易求此三角形的面积.
与两坐标轴围成的三角形是直角三角形,故易求此三角形的面积.
试题解析:(1)解法一:联立两直线方程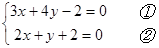 解得
解得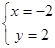 ,则两直线的交点为P(-2,2),又因为直线
,则两直线的交点为P(-2,2),又因为直线 的斜率为
的斜率为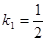 ,由于所求直线
,由于所求直线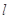 与直线
与直线 垂直,那么直线
垂直,那么直线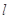 的斜率
的斜率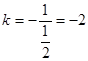 ,故所求直线
,故所求直线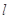 的方程为:
的方程为: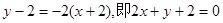 ;
;
解法二:由直线系方程,由已知可设所求直线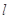 的方程为:
的方程为: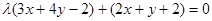 即
即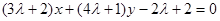 与直线
与直线 垂直,所以
垂直,所以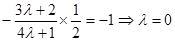 ,故所求直线
,故所求直线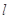 的方程为:
的方程为: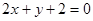 ;
;
(2)对于直线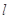 的方程为:
的方程为: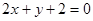 ,令y=0,则x=-1,即直线
,令y=0,则x=-1,即直线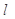 与x轴的交点坐标A(-1,0),再令x=0则y="-2," 即直线
与x轴的交点坐标A(-1,0),再令x=0则y="-2," 即直线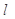 与y轴的交点坐标B(0,-2);从而直线
与y轴的交点坐标B(0,-2);从而直线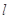 与两坐标轴围成的三角形为直角三角形AOB
与两坐标轴围成的三角形为直角三角形AOB 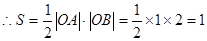 .
.
考点:直线方程.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
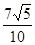 .
.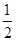 ;
;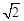 ∶
∶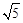 .若能,求P点坐标;若不能,说明理由.
.若能,求P点坐标;若不能,说明理由.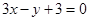 上,若⊿ABC的面积为10,求C点的坐标.
上,若⊿ABC的面积为10,求C点的坐标.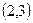 射到
射到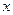 轴上点
轴上点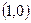 ,经
,经 :
: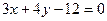 和
和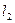 :
: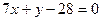 ,则直线
,则直线 夹角为________
夹角为________