题目内容
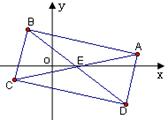
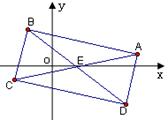
如图,已知长方形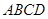 的两条对角线的交点为
的两条对角线的交点为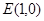 ,且
,且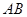 与
与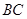 所在的直线方程分别为
所在的直线方程分别为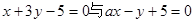 .
.
(1)求 所在的直线方程;
所在的直线方程;
(2)求出长方形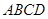 的外接圆的方程.
的外接圆的方程.
(1)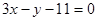
(2)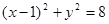
解析试题分析:(1)由已知条件推导出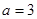 ,设
,设 所在的直线
所在的直线
方程为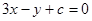 ,由
,由 到
到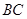 的距离和
的距离和 到
到 的距离相等,能求出
的距离相等,能求出 所在的直线方程.
所在的直线方程.
(2)由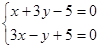 ,得
,得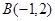 ,从而得到
,从而得到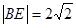 ,由此能求出长方形
,由此能求出长方形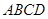 的外接圆的方程.
的外接圆的方程.
试题解析:(1)由于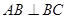 ,则
,则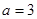
由于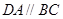 ,则可设直线
,则可设直线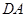 的方程为:
的方程为: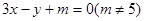 ,
,
又点 到
到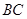 与
与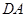 的距离相等,则
的距离相等,则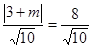 ,
,
因此,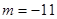 ,或
,或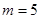 (舍去),
(舍去),
则直线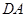 所在的方程为
所在的方程为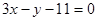 .
.
(2)由直线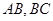 的方程解出点
的方程解出点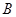 的坐标为
的坐标为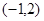 ,则
,则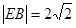 即为长方形
即为长方形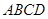 的外接圆半径.
的外接圆半径.
故长方形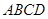 的外接圆的方程为
的外接圆的方程为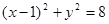 .
.
考点:圆的标准方程;直线的一般式方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
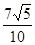 .
.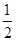 ;
;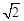 ∶
∶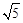 .若能,求P点坐标;若不能,说明理由.
.若能,求P点坐标;若不能,说明理由.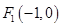 、
、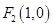 ,动点
,动点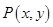 ,且满足
,且满足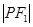 、
、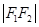 、
、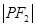
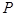 的轨迹
的轨迹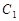 的方程;
的方程;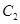 的方程为
的方程为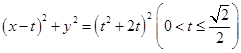 ,过点
,过点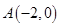 的直线
的直线 与曲线
与曲线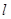 被曲线
被曲线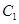 截得的线段长的最小值.
截得的线段长的最小值.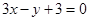 上,若⊿ABC的面积为10,求C点的坐标.
上,若⊿ABC的面积为10,求C点的坐标.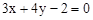 ;
;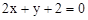 ,它的中心为M
,它的中心为M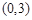 ,求平行四边形另外两条边CB、CD所在的直线方程及平行四边形的面积.
,求平行四边形另外两条边CB、CD所在的直线方程及平行四边形的面积.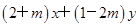 +4-3m=0.
+4-3m=0.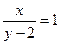 表示斜率为1,在y轴上的截距为2的直线
表示斜率为1,在y轴上的截距为2的直线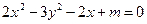 过原点的充分必要条件是m=0
过原点的充分必要条件是m=0