题目内容
已知lg(3x)+lgy=lg(x+y+1).
(1)求xy的最小值;
(2)求x+y的最小值.
(1)求xy的最小值;
(2)求x+y的最小值.
(1)1 (2)2
解:由lg(3x)+lgy=lg(x+y+1)得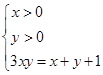
(1)∵x>0,y>0,
∴3xy=x+y+1≥2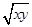 +1,
+1,
∴3xy-2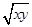 -1≥0,
-1≥0,
即3(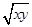 )2-2
)2-2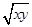 -1≥0,
-1≥0,
∴(3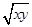 +1)(
+1)(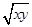 -1)≥0,
-1)≥0,
∴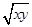 ≥1,∴xy≥1,
≥1,∴xy≥1,
当且仅当x=y=1时,等号成立.
∴xy的最小值为1.
(2)∵x>0,y>0,
∴x+y+1=3xy≤3·(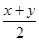 )2,
)2,
∴3(x+y)2-4(x+y)-4≥0,
∴[3(x+y)+2][(x+y)-2]≥0,
∴x+y≥2,
当且仅当x=y=1时取等号,
∴x+y的最小值为2.
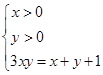
(1)∵x>0,y>0,
∴3xy=x+y+1≥2
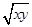 +1,
+1,∴3xy-2
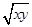 -1≥0,
-1≥0,即3(
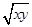 )2-2
)2-2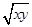 -1≥0,
-1≥0,∴(3
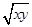 +1)(
+1)(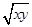 -1)≥0,
-1)≥0,∴
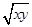 ≥1,∴xy≥1,
≥1,∴xy≥1,当且仅当x=y=1时,等号成立.
∴xy的最小值为1.
(2)∵x>0,y>0,
∴x+y+1=3xy≤3·(
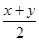 )2,
)2,∴3(x+y)2-4(x+y)-4≥0,
∴[3(x+y)+2][(x+y)-2]≥0,
∴x+y≥2,
当且仅当x=y=1时取等号,
∴x+y的最小值为2.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
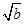 =4,则
=4,则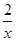 +
+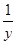 的最大值为( )
的最大值为( )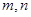 是正实数,且点
是正实数,且点 在曲线
在曲线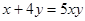 上,则
上,则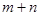 的最小值是 .
的最小值是 .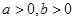 ,且
,且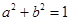 ,则下列结论中正确的是
,则下列结论中正确的是 (填上所有正确结论得序号)
(填上所有正确结论得序号)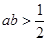 ;②
;②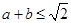 ;③
;③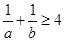 ;④
;④ ;⑤
;⑤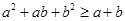 .
.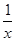
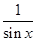 ,x∈
,x∈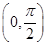
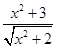
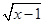 +
+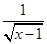
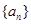 ,
,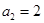 ,则其前三项和
,则其前三项和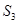 的取值范围是( )
的取值范围是( )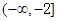
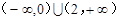
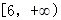
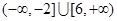
 +
+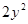 的最小值为______________.
的最小值为______________.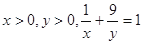 时,
时,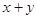 的最小值为( )
的最小值为( )