题目内容
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,
OC=OE=4,DB⊥DC,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交
于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.

(1)求经过B、E、C三点的抛物线的解析式;
(2)是否存在点P,使得以P、Q、M为顶点的三角形与△AOD相似?若存在,求出满足条件
的点P的坐标;若不存在,请说明理由;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成
为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
OC=OE=4,DB⊥DC,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交
于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.

(1)求经过B、E、C三点的抛物线的解析式;
(2)是否存在点P,使得以P、Q、M为顶点的三角形与△AOD相似?若存在,求出满足条件
的点P的坐标;若不存在,请说明理由;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成
为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
(1) y=-(x+1)(x-4)=-x2+3x+4 (2)存在符合条件的P点 (3)存在
试题分析:(1)在R t △BDC中,OD⊥BC, 由射影定理,得:OD2=OB•OC; 则OB=OD2
÷OC=1;∴B(-1,0); ∴B(-1,0),C(4,0),E(0,4); 设抛物线的解析式为:
y=a(x+1)(x-4)(a≠0),则有: a(0+1)(0-4)=4,a=-1;∴y=-(x+1)(x-4)=-x2+3x+4;
(2)因为A(-2,0),D(0,2); 所以直线AD:y=x+2; 联立抛物线的解析式可求得F
(1-
 ,3-
,3- ),G(1+
),G(1+  ,3+
,3+  ); 设P点坐标为(x,x+2)(1-
); 设P点坐标为(x,x+2)(1-  <x<
<x<1+
 ),则Q(x,-x2+3x+4); ∴PQ=-x2+3x+4-x-2=-x2+2x+2; 易知M(
),则Q(x,-x2+3x+4); ∴PQ=-x2+3x+4-x-2=-x2+2x+2; 易知M(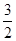 ,
,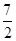 )。 若
)。 若以P、Q、M为顶点的三角形与△AOD相似,则△PQM为等腰直角三角形; ①以M为直
角顶点,PQ为斜边,则P(2-
 ,4-
,4-  ); ②以Q为直角顶点,PM为斜边;
); ②以Q为直角顶点,PM为斜边;P(
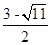 ,
,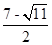 )故存在符合条件的P点,且P点坐标为(2-
)故存在符合条件的P点,且P点坐标为(2-  ,4-
,4-  )
)或(
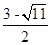 ,
,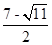 );(3)易知N(
);(3)易知N(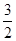 ,
,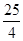 ),M(
),M(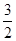 ,
,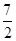 ); 设P点
); 设P点坐标为(m,m+2), 则Q(m,-m2+3m+4);(1-
 <m<1+
<m<1+  ) ∴PQ=-m2+2m+2,
) ∴PQ=-m2+2m+2,NM=
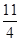 ; ①若四边形PMNQ是菱形,则首先四边形PMNQ是平行四边形,有: MN=PQ,
; ①若四边形PMNQ是菱形,则首先四边形PMNQ是平行四边形,有: MN=PQ,即:-m2+2m+2=
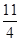 , 解得m=
, 解得m= 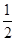 ,m=
,m= 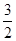 (舍去);当m=
(舍去);当m=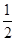 时,P(
时,P(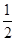 ,
,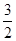 ),Q
),Q(
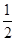 ,
, ) 此时PM≠MN,故四边形PMNQ不可能是菱形; ②由于当NQ∥PM时,
) 此时PM≠MN,故四边形PMNQ不可能是菱形; ②由于当NQ∥PM时,四边形PMNQ是平行四边形,所以若四边形PMNQ是梯形,只有一种情况:PQ∥MN,此
时P点坐标为(
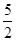 ,
,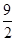 ).
).∴四边形PMNQ可以是等腰梯形,且P点坐标为(
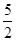 ,
,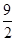 ).
).点评:此题是二次函数的综合题,考查的知识点有:直角三角形的性质,二次函数的确定,
等腰三角形、菱形、等腰梯形的判定和性质等,同时还考查了分类讨论的数学思想;要特别
注意的是在判定梯形的过程中,不要遗漏证明另一组对边不平行的条件.

练习册系列答案
相关题目

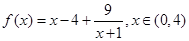 ,当
,当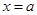 时,
时,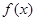 取得最小值
取得最小值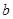 ,则函数
,则函数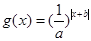 的图象为( )
的图象为( )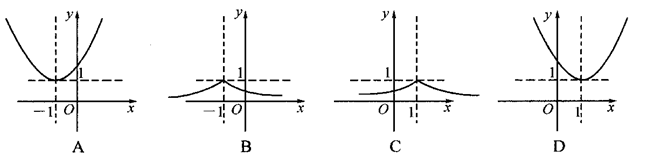
 (
( )的图象如图.根据图象写出:
)的图象如图.根据图象写出:
 的
的 值.
值. 是以2为周期的偶函数,当
是以2为周期的偶函数,当 时,
时, ,且在
,且在 内,关于
内,关于 的方程
的方程 有四个根,则
有四个根,则 得取值范围是
得取值范围是  的图像与函数
的图像与函数 的图像没有公共点,则实数
的图像没有公共点,则实数 的取值范围是____________.
的取值范围是____________.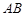 的长为
的长为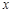 ,
,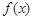 表示弧
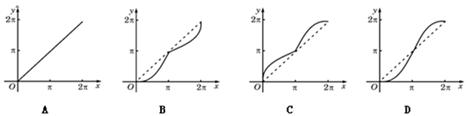
表示弧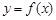 的图象是( )
的图象是( ) 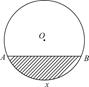
 在
在 上是增函数,则二次函数
上是增函数,则二次函数 的图象可以为( ).
的图象可以为( ).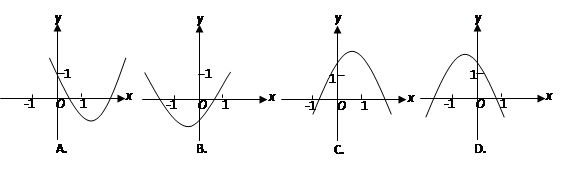
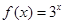 ,
,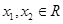 ,则有:( )
,则有:( )

