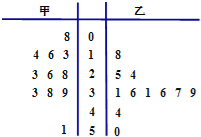
题目内容
【题目】家政服务公司根据用户满意程度将本公司家政服务员分为两类,其中A类服务员12名,B类服务员![]() 名
名
(1)若采用分层抽样的方法随机抽取20名家政服务员参加技术培训,抽取到B类服务员的人数是16, 求![]() 的值
的值
(2)某客户来公司聘请2名家政服务员,但是由于公司人员安排已经接近饱和,只有3名A类家政服务员和2名B类家政服务员可供选择
①请列出该客户的所有可能选择的情况
②求该客户最终聘请的家政服务员中既有A类又有B类的概率来源:学|科|网]
【答案】解: (1)20-16=4, 由![]() ,可得
,可得![]() =48
=48
(2) ①设3名A类家政服务员的编号为a,b,c,2名B类家政服务员的编号为1,2,
则所有可能情况有:
(a,b),(a,c),(a,1),(a,2),(b,c),(b,1),(b,2),(c,1),(c,2),(1,2)共10种选择.
②该客户最终聘请的家政服务员中既有A类又有B类的情况有:
(a,1),(a,2),(b,1),(b,2),(c,1),(c,2)共6种选择,
![]() 该客户最终聘请的家政服务员中既有A类又有B类的概率为
该客户最终聘请的家政服务员中既有A类又有B类的概率为![]()
【解析】
试题分析:(1)根据分层抽样比例求x的值,
(2)列举出所有的可能,找到满足最终聘请的家政服务员中既有A类又有B类的情况,根据古典概率公式计算即可.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】高一学年结束后,要对某班的50名学生进行文理分班,为了解数学对学生选择文理科是否有影响,有人对该班的分科情况做了如下的数据统计:
理科人数 | 文科人数 | 总计 | |
数学成绩好的人数 | 25 | 30 | |
数学成绩差的人数 | 10 | ||
合计 | 15 |
(Ⅰ)根据数据关系,完成![]() 列联表;
列联表;
(Ⅱ)通过计算判断能否在犯错误的概率不超过![]() 的前提下认为数学对学生选择文理科有影响.
的前提下认为数学对学生选择文理科有影响.
附:![]()
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
【题目】进入冬天,大气流动性变差,容易形成雾握天气,从而影响空气质量.某城市环保部门试图探究车流量与空气质量的相关性,以确定是否对车辆实施限行.为此,环保部门采集到该城市过去一周内某时段车流量与空气质量指数的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
车流量(x万辆) | 10 | 9 | 9.5 | 10.5 | 11 | 8 | 8.5 |
空气质量指数y | 78 | 76 | 77 | 79 | 80 | 73 | 75 |
(1)根据表中周一到周五的数据,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2,则认为得到的线性回归方程是可靠的.请根据周六和周日数据,判定所得的线性回归方程是否可靠?
附:回归方程![]() 中斜率和截距最小二乘估计公式分别为:
中斜率和截距最小二乘估计公式分别为:
 其中:
其中:![]()
![]()