题目内容
设数列{an}的前n项和为Sn,且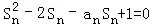 ,n=1,2,3
,n=1,2,3
(1)求a1,a2;
(2)求Sn与Sn﹣1(n≥2)的关系式,并证明数列{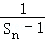 }是等差数列;
}是等差数列;
(3)求S1•S2•S3 S2011•S2012的值.
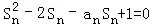 ,n=1,2,3
,n=1,2,3 (1)求a1,a2;
(2)求Sn与Sn﹣1(n≥2)的关系式,并证明数列{
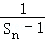 }是等差数列;
}是等差数列;(3)求S1•S2•S3 S2011•S2012的值.
(1)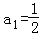 ,
,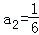 ;(2)SnSn﹣1﹣2Sn+1=0;(3)
;(2)SnSn﹣1﹣2Sn+1=0;(3)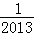 .
.
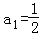 ,
,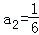 ;(2)SnSn﹣1﹣2Sn+1=0;(3)
;(2)SnSn﹣1﹣2Sn+1=0;(3)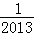 .
.试题分析:(1)直接利用
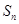 与
与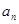 的关系式求
的关系式求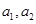 的值;(2)当
的值;(2)当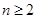 时,把
时,把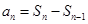 代入已知关系式可得与
代入已知关系式可得与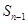 的关系式,再由此关系式,去凑出
的关系式,再由此关系式,去凑出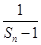 和
和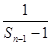 ,可得所求数列
,可得所求数列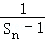 是等差数列,进而得通项
是等差数列,进而得通项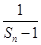 的表达式,从而得
的表达式,从而得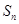 的表达式;(3)由(2)中
的表达式;(3)由(2)中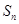 的表达式易求S1•S2•S3 S2011•S2012的值.
的表达式易求S1•S2•S3 S2011•S2012的值.试题解析:(1)解:当n=1时,由已知得
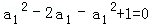 ,解得
,解得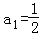 ,
,同理,可解得
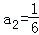 . (4分)
. (4分)(2)证明:由题设
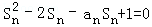 ,
,当n≥2时,an=Sn﹣Sn﹣1,代入上式,得SnSn﹣1﹣2Sn+1=0,
∴
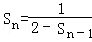 , (7分)
, (7分)∴
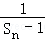 =﹣1+
=﹣1+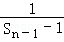 ,
,∴{
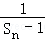 }是首项为
}是首项为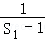 =﹣2,公差为﹣1的等差数列, (10分)
=﹣2,公差为﹣1的等差数列, (10分)∴
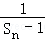 =﹣2+(n﹣1)•(﹣1)=﹣n﹣1,∴Sn=
=﹣2+(n﹣1)•(﹣1)=﹣n﹣1,∴Sn=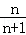 . (12分)
. (12分)(3)解:S1•S2•S3 S2011•S2012=
 •
•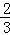 •
•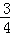 •
•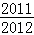 •
•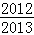 =
=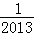 . (14分)
. (14分)
练习册系列答案
相关题目
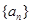 的前
的前 项和为
项和为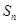 ,
,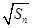 是
是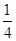 与
与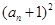 的等比中项.
的等比中项.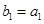 ,且
,且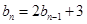 ,求数列
,求数列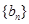 的通项公式;
的通项公式;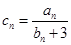 ,求数列
,求数列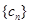 的前
的前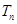 .
.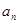 }中,
}中,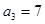 ,又
,又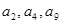 成等比数列.
成等比数列.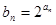 ,求数列{
,求数列{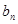 }的前n项和
}的前n项和 .
.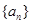 中,
中,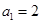 ,
, 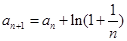 ,则
,则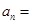 ( )
( )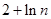
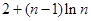
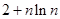
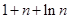
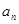 }的前n项和为
}的前n项和为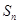 ,且
,且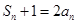 ,则使不等式
,则使不等式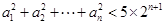 成立的n的最大值为 .
成立的n的最大值为 .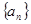 的公差
的公差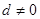 ,且
,且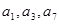 成等比数列,则
成等比数列,则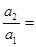 ( )
( )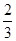
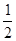
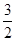
 的前
的前 项和为
项和为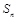 ,若
,若 ,
,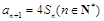 ,则
,则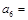 ( )
( )



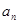 }是等差数列,a4+a6=6,其前5项和S5=10,则其公差d=___________.
}是等差数列,a4+a6=6,其前5项和S5=10,则其公差d=___________.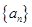 中,若
中,若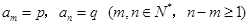 ,则
,则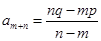 .
.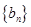 (
(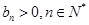 ),若
),若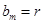 ,
,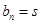 (
(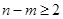 ,
,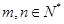 ),则可以得到
),则可以得到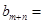 .
.