题目内容
6.已知向量$\overrightarrow{a},\overrightarrow{b}$,满足|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,且($\overrightarrow{a}$-$\frac{5}{2}$$\overrightarrow{b}$)⊥($\overrightarrow{a}$+$\overrightarrow{b}$),则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ为$\frac{π}{3}$.分析 由条件利用两个向量垂直的性质,两个向量的数量积的定义求得cosθ的值,可得$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ的值.
解答 解:由题意可得($\overrightarrow{a}$-$\frac{5}{2}$$\overrightarrow{b}$)•($\overrightarrow{a}$+$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}$-$\frac{3}{2}$$\overrightarrow{a}•\overrightarrow{b}$-$\frac{5}{2}$${\overrightarrow{b}}^{2}$=4-$\frac{3}{2}$$\overrightarrow{a}•\overrightarrow{b}$-$\frac{5}{2}$=0,
解得$\overrightarrow{a}$•$\overrightarrow{b}$=1,∴2×1×cosθ=1,∴cosθ=$\frac{1}{2}$,求得θ=$\frac{π}{3}$,
故答案为:$\frac{π}{3}$.
点评 本题主要考查两个向量的数量积的定义,两个向量垂直的性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知x∈R,a<lg(|x-3|+|x+7|)恒成立,则a的取值范围是( )
| A. | a≥1 | B. | a>1 | C. | a≤1 | D. | a<1 |
14.若曲线C上的点到椭圆 $\frac{{x}^{2}}{1{3}^{2}}$+$\frac{{y}^{2}}{1{2}^{2}}$=1的两个焦点的距离的差的绝对值等于8,则曲线C的标准方程为( )
| A. | $\frac{{x}^{2}}{1{3}^{2}}$-$\frac{{y}^{2}}{1{2}^{2}}$=1 | B. | $\frac{{x}^{2}}{1{3}^{2}}$-$\frac{{y}^{2}}{{5}^{2}}$=1 | ||
| C. | $\frac{{x}^{2}}{{3}^{2}}$-$\frac{{y}^{2}}{{4}^{2}}$=1 | D. | $\frac{{x}^{2}}{{4}^{2}}$-$\frac{{y}^{2}}{{3}^{2}}$=1 |
1.b=-1是直线y=x+b过抛物线y2=4x焦点的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.如图,在公路MN的两侧有四个村镇:A1、B1、C1、D1通过小路和公路相连,各路口分别是A、B、C、D,现要在公路上建一个长途汽车站,为使各村镇村民到汽车站所走的路程总和最小,汽车站应建在( )
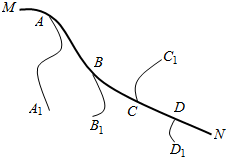

| A. | A处 | B. | D处 | ||
| C. | B、C间的任何一处(包括B、C) | D. | A、B之间的任何一处(包括A、B) |
18.由函数y=lg(1-2x)的图象得到函数y=lg(3-2x)的图象,只需要( )
| A. | 向左平移1个单位 | B. | 向右平移1个单位 | C. | 向左平移2个单位 | D. | 向右平移2个单位 |
15.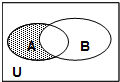 已知全集U=R,集合A={x|x>1},集合B={x|3x-4≤0},满足如图所示的阴影部分的集合是( )
已知全集U=R,集合A={x|x>1},集合B={x|3x-4≤0},满足如图所示的阴影部分的集合是( )
 已知全集U=R,集合A={x|x>1},集合B={x|3x-4≤0},满足如图所示的阴影部分的集合是( )
已知全集U=R,集合A={x|x>1},集合B={x|3x-4≤0},满足如图所示的阴影部分的集合是( )| A. | {x|x>1} | B. | {x|1<x≤$\frac{4}{3}$} | C. | {x|x≤1} | D. | {x|x>$\frac{4}{3}$} |
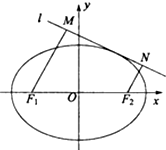 已知两点F1(-1,0),F2(1,0),点P在以F1,F2为焦点的椭圆C,且|PF1|,|F1F2|,|PF2|构成等差数列.
已知两点F1(-1,0),F2(1,0),点P在以F1,F2为焦点的椭圆C,且|PF1|,|F1F2|,|PF2|构成等差数列.