题目内容

1．b=-1是直线y=x+b过抛物线y2=4x焦点的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

分析 根据充分条件和必要条件的定义结合抛物线的性质进行判断即可．

解答 解：抛物线y2=4x的焦点坐标为（1，0），
若是直线y=x+b过抛物线y2=4x的焦点，
则1+b=0，解得b=-1，
即b=-1是直线y=x+b过抛物线y2=4x焦点的充要条件，
故选：C

点评 本题主要考查充分条件和必要条件的判断，根据抛物线的性质是解决本题的关键．

练习册系列答案
相关题目
10．已知全集U=R集合A={x|log2（x-1）}，B={y|y=2x}，则（CUA）∩B=（　　）
A．（-∞，0）B．（0，1]C．（-∞，1）D．（1，2）
12．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）及内部面积为S=πab，A1，A2是长轴的两个顶点，B1，B2是短轴的两个顶点，在椭圆上或椭圆内部随机取一点 P，给出下列命题：
①△PA1A2为钝角三角形的概率为1；
②△PB1B2为钝角三角形的概率为$\frac{b}{a}$；
③△PA1A2为钝角三角形的概率为$\frac{b}{a}$； 
④△PB1B2为锐角三角形的概率为$\frac{a-b}{a}$．
其中正确的命题有①②④．（填上你认为所有正确的命题序号）
9．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，一个焦点与抛物线y2=4x的焦点重合，直线l：y=kx+m与椭圆C相交于A、B两点．
（1）求椭圆C的标准方程；
（2）设O为坐标原点，kOA•kOB=-$\frac{{b}^{2}}{{a}^{2}}$，判断△AOB的面积是否为定值？若是，求出定值，若不是，说明理由．
16．若椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，点（1，$\frac{3}{2}$）在椭圆C上．
（1）求椭圆C的方程；
（2）过椭圆右焦点F2 斜率为k（k≠0的直线l与椭圆C相交于E，F两点，A为椭圆的右顶点，直线AE，AF分别交直线x=3于点M，N，线段MN的中点为P，记直线PF2 的斜率为k′，求证：k•k′为定值．
6．已知向量$\overrightarrow{a}，\overrightarrow{b}$，满足|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=1，且（$\overrightarrow{a}$-$\frac{5}{2}$$\overrightarrow{b}$）⊥（$\overrightarrow{a}$+$\overrightarrow{b}$），则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ为$\frac{π}{3}$．
13．已知函数f（x）的对应关系如表所示，则f[f（5）]的值为（　　）
x12345
f（x）54312
A．1B．2C．4D．5
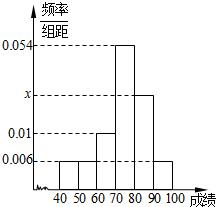10．某班50位学生期中考试数学成绩的频率分布直方图如图所示．
（1）求图中x的值；
（2）试估计这50名学生的平均成绩（同一组中的数据用该组区间的中点值作代表）
11．在同一坐标中，方程a2x2+b2y2=1与ax+by2=0（a＞b＞9）的曲线大致是（　　）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网