题目内容
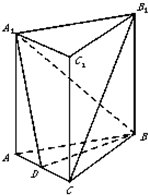
如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC=3,AC=2,D是AC的中点.
(Ⅰ)求证:B1C∥平面A1BD;
(Ⅱ)求二面角A1-BD-B1的余弦值.
(Ⅰ)求证:B1C∥平面A1BD;
(Ⅱ)求二面角A1-BD-B1的余弦值.

(Ⅰ)连结AB1,交A1B于点O,连结OD,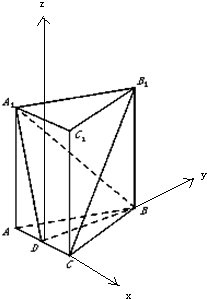
∵在直三棱柱ABC-A1B1C1中,AA1=AB=BC=3,
∴ABB1A1是正方形,∴O是AB1的中点,
∵D是AC的中点,∴OD是△ACB1的中位线,∴OD∥B1C,
∵B1C不包含于平面A1BD,OD?平面A1BD,
∴B1C∥平面A1BD.
(Ⅱ)以D为坐标原点,以DC为x轴,以DB为y轴,
以过D点垂直于AC的直线为z轴,建立空间直角坐标系,
∵AA1=AB=BC=3,AC=2,D是AC的中点,
∴A1(-1,0,3),B(0,2
,0),
D(0,0,0),B1(0,2
,3),
∴
=(-1,0,3),
=(0,2
,0),
=(0,2
,3),
设平面A1BD的法向量
=(x,y,z),则
•
=0,
•
=0,
∴
,∴
=(3,0,1),
设平面B1BD的法向量
=(x1,y1,z1),则
•
=0,
•
=0,
∴
,∴
=(1,0,0),
设二面角A1-BD-B1的平面角为θ,
cosθ=|cos<
,
>|=|
|=
.
∴二面角A1-BD-B1的余弦值为
.

∵在直三棱柱ABC-A1B1C1中,AA1=AB=BC=3,
∴ABB1A1是正方形,∴O是AB1的中点,
∵D是AC的中点,∴OD是△ACB1的中位线,∴OD∥B1C,
∵B1C不包含于平面A1BD,OD?平面A1BD,
∴B1C∥平面A1BD.
(Ⅱ)以D为坐标原点,以DC为x轴,以DB为y轴,
以过D点垂直于AC的直线为z轴,建立空间直角坐标系,
∵AA1=AB=BC=3,AC=2,D是AC的中点,
∴A1(-1,0,3),B(0,2
| 2 |
D(0,0,0),B1(0,2
| 2 |
∴
| DA1 |
| DB |
| 2 |
| DB1 |
| 2 |
设平面A1BD的法向量
| m |
| m |
| DA1 |
| m |
| DB |
∴
|
| m |
设平面B1BD的法向量
| n |
| n |
| DB1 |
| n |
| DB |
∴
|
| n |
设二面角A1-BD-B1的平面角为θ,
cosθ=|cos<
| m |
| n |
| 3 | ||
|
3
| ||
| 10 |
∴二面角A1-BD-B1的余弦值为
3
| ||
| 10 |

练习册系列答案
相关题目






 与
与 满足
满足 ,
, ,若存在实数
,若存在实数 ,使得
,使得 垂直,则
垂直,则
 =(1,2),
=(1,2),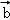 =(﹣2,y),若
=(﹣2,y),若 ﹣
﹣ |等于( )
|等于( )
