题目内容
关于函数f(x)=4sin(2x+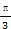
)(x∈R),有下列命题:
①由f(x1)=f(x2)=0可得x1-x2必是π的整数倍;
②y=f(x)的表达式可改写为y="4" cos(2x-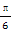
);
③y=f(x)的图象关于点(-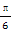,0)对称;
④y=f(x)的图象关于直线x=-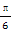对称.
其中正确命题的序号是 .
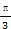)(x∈R),有下列命题:①由f(x1)=f(x2)=0可得x1-x2必是π的整数倍;
②y=f(x)的表达式可改写为y="4" cos(2x-
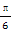);③y=f(x)的图象关于点(-
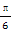,0)对称;④y=f(x)的图象关于直线x=-
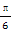对称.其中正确命题的序号是 .
②③
①错,∵当x1=-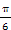
,x2=
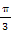时,f(x1)=f(x2)=0,而x1-x2=-
.
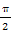②对,∵y=4cos(2x-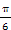)=4cos[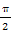-(2x+)]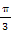
=4sin(2x+).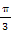
③对,∵当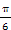x=-时,2x+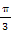=0,此时f(x)=0,
故f(x)的图象关于(-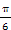,0)成中心对称.
④错,由③可知x=-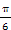不是y=f(x)的图象的对称轴.
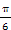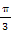,x2=时,f(x1)=f(x2)=0,而x1-x2=-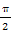.②对,∵y=4cos(2x-
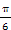)=4cos[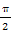-(2x+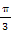)]=4sin(2x+
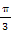).③对,∵当x=-
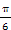时,2x+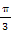=0,此时f(x)=0,故f(x)的图象关于(-
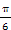,0)成中心对称.④错,由③可知x=-
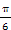不是y=f(x)的图象的对称轴.
练习册系列答案
每课必练系列答案
巧学巧练系列答案
相关题目
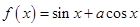的图象经过点
.
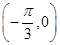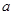的值；
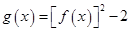，求函数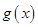
的最小正周期与单调递增区间.
．
的最小正周期和值域；
，
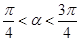.求
的值．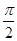
个单位后，与函数y＝sin
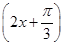的图象重合，则φ＝________．
sin2x-
-
.
,
],求函数f(x)的最值及对应的x的值.
)的图象经过点(0,1),且
一个最高点的坐标为(1,2),则ω的最小值是 .
对称,则|φ|的最小值是( )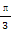
)在[0,
]上的最大值为M,最小值为m,则M+m等于( )
cos 2x的最小正周期T＝________，振幅A＝________.