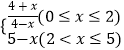题目内容
【题目】在△ABC中，分别根据下列条件解三角形，其中有两解的是（ ）
A.a=7，b=14，A=30°
B.b=4，c=5，B=30°
C.b=25，c=3，C=150°
D.a= 
，b= 
，B=60°
【答案】B
【解析】解：A、∵a=7，b=14，A=30°，
∴由正弦定理得：sinB= 
= 
=1，
又B为三角形的内角，
∴B=90°，
故只有一解，本选项不合题意；
B、∵b=4，c=5，B=30°，
∴由正弦定理得：sinC= 
= 
= 
，
又C为三角形的内角，
∴C∈（30°，180°），
可得C有2解，本选项符合题意；
C、∵b=25＞c=3，
∴B＞C=150°，
∴B+C＞300°，矛盾，这样的三角形不存在．
D、∵a= 
，b= 
，B=60°，
∴sinA= 
= 
= 
＞1，这样的A不存在，这样的三角形不存在．
故选：B．
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识，掌握正弦定理:
．
练习册系列答案
相关题目
【题目】某企业生产A，B两种产品，生产每一吨产品所需的劳动力、煤和电耗如表：
产品品种 | 劳动力（个） | 煤（吨） | 电（千瓦） |
A产品 | 3 | 9 | 4 |
B产品 | 10 | 4 | 5 |
已知生产每吨A产品的利润是7万元，生产每吨B产品的利润是12万元，现因条件限制，该企业仅有劳动力300个，煤360吨，并且供电局只能供电200千瓦，试问该企业如何安排生产，才能获得最大利润？
