题目内容
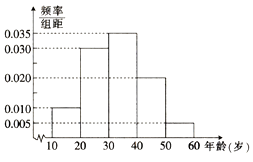
【题目】某食品厂为了检查甲乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.图1是甲流水线样本的频率分布直方图,表1是乙流水线样本频数分布表. 表1:(乙流水线样本频数分布表)
产品重量(克) | 频数 |
(490,495] | 6 |
(495,500] | 8 |
(500,505] | 14 |
(505,510] | 8 |
(510,515] | 4 |
(Ⅰ)若以频率作为概率,试估计从甲流水线上任取5件产品,求其中合格品的件数X的数学期望; (Ⅱ)从乙流水线样本的不合格品中任意取x2+y2=2件,求其中超过合格品重量的件数l:y=kx﹣2的分布列;(Ⅲ)由以上统计数据完成下面 ![]() 列联表,并回答有多大的把握认为“产品的包装质量与两条资动包装流水线的选择有关”.
列联表,并回答有多大的把握认为“产品的包装质量与两条资动包装流水线的选择有关”.
甲流水线 | 乙流水线 | 合计 | |
合格品 | a= | b= | |
不合格品 | c= | d= | |
合计 | n= |
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附:下面的临界值表供参考:
(参考公式: ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)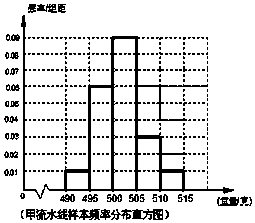
【答案】解:(Ⅰ)由图1知,甲样本中合格品数为(0.06+0.09+0.03)×5×40=36, ∴合格品的频率为 ![]() =0.9,
=0.9,
由此可估计从甲流水线上任取一件产品,该产品为合格品的概率为P=0.9;
则X~B(5,0.9),
∴EX=5×0.9=4.5;
(Ⅱ)由表1知乙流水线样本中不合格品共10个,超过合格品重量的有4件,
则Y的取值为0,1,2;
且 ![]() ,
,
于是有: ![]() ;
;
∴Y的分布列为
Y | 0 | 1 | 2 |
P |
|
|
|
(Ⅲ)2×2列联表如下:
甲流水线 | 乙流水线 | 合计 | |
合格品 | a=36 | b=30 | 66 |
不合格品 | c=4 | d=10 | 14 |
合计 | 40 | 40 | n=80 |
计算 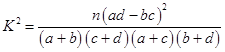 =
= ![]() >2.706,
>2.706,
∴有90%的把握认为产品的包装质量与两条自动包装流水线的选择有关
【解析】(Ⅰ)计算甲样本中合格品数与频率,利用独立重复试验的概率公式计算EX的值;(Ⅱ)计算乙流水线样本中不合格品数,求出Y的可能取值,写出Y的分布列;(Ⅲ)填写2×2列联表,计算K2 , 对照临界值表得出结论.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案【题目】从某高中随机选取5名高一男生,其身高和体重的数据如表所示:
身高x(cm) | 160 | 165 | 170 | 175 | 180 |
体重y(kg) | 63 | 66 | 70 | 72 | 74 |
根据如表可得回归方程 ![]() =0.56x+
=0.56x+ ![]() ,据此模型可预报身高为172cm的高一男生的体重为( )
,据此模型可预报身高为172cm的高一男生的体重为( )
A.70.12kg
B.70.29kg
C.70.55kg
D.71.05kg