题目内容
【题目】已知圆P过A（﹣8，0），B（2，0），C（0，4）三点，圆Q：x2+y2﹣2ay+a2﹣4=0．
（1）求圆P的方程；
（2）如果圆P和圆Q相外切，求实数a的值．
【答案】
（1）解：设圆P的方程为x2+y2+Dx+Ey+F=0，
∵圆P过A（﹣8，0），B（2，0），C（0，4）三点，
∴ 
，解得D=6，E=0，F=﹣16，
∴圆P的方程为x2+y2+6x﹣16=0．
（2）解：圆P的方程即（x+3）2+y2=25，∴圆心P（﹣3，0），半径r=5，
圆Q：x2+y2﹣2ay+a2﹣4=0，即x2+（y﹣a）2=4，
圆心Q（0，a），半径r=2，
∵圆P和圆Q相外切，∴|PQ|=5+2=7，
∴（﹣3﹣0）2+（0﹣a）2=72，
解得a= 
．
【解析】（1）设圆P的方程为x2+y2+Dx+Ey+F=0，利用待宝系数法能求出圆P的方程．（2）圆P的圆心P（﹣3，0），半径r=5，圆Q的圆心Q（0，a），半径r=2，由圆P和圆Q相外切，得|PQ|=5+2=7，由此利用两点间距离公式能求出a．
【考点精析】解答此题的关键在于理解圆的标准方程的相关知识，掌握圆的标准方程：
；圆心为A(a,b),半径为r的圆的方程．
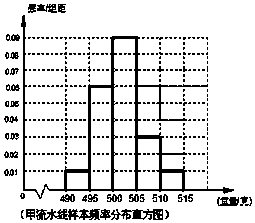
【题目】某食品厂为了检查甲乙两条自动包装流水线的生产情况，随机在这两条流水线上各抽取40件产品作为样本称出它们的重量（单位：克），重量值落在（495，510]的产品为合格品，否则为不合格品．图1是甲流水线样本的频率分布直方图，表1是乙流水线样本频数分布表． 表1：（乙流水线样本频数分布表）
产品重量（克） | 频数 |
（490，495] | 6 |
（495，500] | 8 |
（500，505] | 14 |
（505，510] | 8 |
（510，515] | 4 |
（Ⅰ）若以频率作为概率，试估计从甲流水线上任取5件产品，求其中合格品的件数X的数学期望； （Ⅱ）从乙流水线样本的不合格品中任意取x2+y2=2件，求其中超过合格品重量的件数l：y=kx﹣2的分布列；（Ⅲ）由以上统计数据完成下面 
列联表，并回答有多大的把握认为“产品的包装质量与两条资动包装流水线的选择有关”．
甲流水线 | 乙流水线 | 合计 | |
合格品 | a= | b= | |
不合格品 | c= | d= | |
合计 | n= |
P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附：下面的临界值表供参考：
（参考公式： 
，其中n=a+b+c+d）
