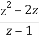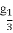题目内容
设数列{an}中,a1=2,an+1=an+n+1,则通项an= .
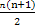 +1
+1
【解析】∵a1=2,an+1=an+n+1,
∴an=an-1+(n-1)+1,an-1=an-2+(n-2)+1,
an-2=an-3+(n-3)+1,…,a3=a2+2+1,
a2=a1+1+1,a1=2=1+1,
将以上各式相加得:
an=[(n-1)+(n-2)+(n-3)+…+2+1]+n+1
=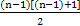 +n+1
+n+1
=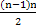 +n+1
+n+1
=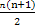 +1.
+1.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目