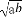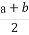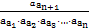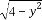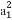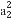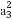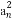题目内容

已知数列{an}满足log3an+1=log3an+1(n∈N*)且a2+a4+a6=9,则lo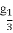(a5+a7+a9)的值是(　　)

(A)-5(B)-(C)5(D)

 

A

【解析】【思路点拨】根据数列满足log3an+1=log3an+1(n∈N*)且a2+a4+a6=9可以确定数列是公比为3的等比数列,再根据等比数列的通项公式即可通过a2+a4+a6=9求出a5+a7+a9的值.

解:由log3an+1=log3an+1(n∈N*),得an+1=3an,又因为an>0,所以数列{an}是公比为3的等比数列,a5+a7+a9=(a2+a4+a6)×33=35,所以lo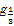(a5+a7+a9)=-log335=-5.

 

练习册系列答案
相关题目

设数列{an}中,a1=2,an+1=an+n+1,则通项an=　　　.

 

设0<a<b,则下列不等式中正确的是(　　)

(A)a<b<< (B)a<<<b

(C)a<<b< (D)<a<<b

 

已知数列{an}满足a1=1,an=3n-1+an-1(n≥2).

(1)求a2,a3.(2)求通项公式an.

 

已知等比数列{an}的首项为2,公比为2,则=　　　.

 

某少数民族的刺绣有着悠久的历史,如图(1)(2)(3)(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.

(1)求出f(5).

(2)利用合情推理的“归纳推理思想”归纳出f(n+1)与f(n)的关系式,并根据你得到的关系式求f(n)的关系式.

 

若在曲线f(x,y)=0上存在两个不同点处的切线重合,则称这条切线为曲线f(x,y)=0的“自公切线”.下列方程:①x2-y2=1;②y=x2-|x|;③y=3sinx+4cosx;④|x|+1=对应的曲线中存在“自公切线”的有(　　)

(A)①② (B)②③

(C)①④ (D)③④

 

数列{an}的前n项和Sn=2n-1,则+++…+等于(　　)

(A)(2n-1)2(B)(2n-1)2

(C)4n-1(D)(4n-1)

 

在等差数列{an}中,已知a4+a8=16,则a2+a10=(　　)

(A)12(B)16(C)20(D)24

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网