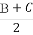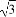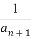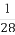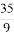题目内容
已知数列{an}为等差数列,公差为d,若 <-1,且它的前n项和Sn有最大值,则使得Sn<0的n的最小值为( )
<-1,且它的前n项和Sn有最大值,则使得Sn<0的n的最小值为( )
(A)11(B)19(C)20(D)21
C
【解析】【思路点拨】解答本题首先要搞清条件“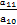 <-1”及“Sn有最大值”如何使用,从而列出关于a1,d的不等式组,求出
<-1”及“Sn有最大值”如何使用,从而列出关于a1,d的不等式组,求出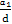 的取值范围,进而求出使得Sn<0的n的最小值,或者根据等比数列的性质求解.
的取值范围,进而求出使得Sn<0的n的最小值,或者根据等比数列的性质求解.
解:方法一:由题意知d<0,a10>0,a11<0, a10+a11<0,
由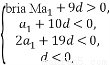 得-
得-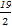 <
<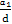 <-9.
<-9.
∵Sn=na1+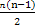 d=
d=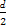 n2+(a1-
n2+(a1-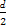 )n,
)n,
由Sn=0得n=0或n=1-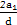 .
.
∵19<1-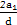 <20,
<20,
∴Sn<0的解集为{n∈N*|n>1-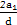 },
},
故使得Sn<0的n的最小值为20.
方法二:由题意知d<0,a10>0,a11<0,a10+a11<0,
由a10>0知S19>0,由a11<0知S21<0,
由a10+a11<0知S20<0,故选C.

练习册系列答案
相关题目