题目内容
12.已知$f(α)=\frac{{sin(α-π)cos(2π-α)cos(-α+\frac{3}{2}π)}}{{cos(\frac{π}{2}-α)sin(-π-α)}}$(1)化简f(α);
(2)若$f(θ-\frac{π}{3})=-\frac{1}{7}$,$-\frac{π}{2}<θ<\frac{π}{2}$,求cos2θ的值.
分析 (1)直接利用诱导公式化简求解即可得到f(α);
(2)利用$f(θ-\frac{π}{3})=-\frac{1}{7}$,$-\frac{π}{2}<θ<\frac{π}{2}$,结合三角函数的基本关系式,求出余弦函数值,然后求cos2θ的值.
解答 解:(1)$f(α)=\frac{{sin(α-π)cos(2π-α)cos(-α+\frac{3}{2}π)}}{{cos(\frac{π}{2}-α)sin(-π-α)}}$=$\frac{sinαcosαsinα}{sinαsinα}$=cosα.
∴f(α)=cosα…(6分)
(2)∵f(α)=cosα,$f(θ-\frac{π}{3})=-\frac{1}{7}$,可得cos($θ-\frac{π}{3}$)=$-\frac{1}{7}$,
$\frac{1}{2}cosθ+\frac{\sqrt{3}}{2}sinθ=-\frac{1}{7}$,sin2θ+cos2θ=1,$-\frac{π}{2}<θ<\frac{π}{2}$,解得$cosθ=\frac{11}{14}$,
∴$cos2θ=2{cos}^{2}θ-1=\frac{23}{98}$…(6分)
点评 本题考查诱导公式的应用,两角和与差的三角函数,考查计算能力.

练习册系列答案
相关题目
3.已知复数z=x+yi(x,y∈R),且|z-2|=$\sqrt{3}$,则$\frac{y+1}{x}$的最大值为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | 2+$\sqrt{6}$ | D. | 2-$\sqrt{6}$ |
7.设θ是△ABC的一个内角,且sinθ+cosθ=$\frac{1}{5}$,x2sinθ-y2cosθ=1表示( )
| A. | 焦点在x轴上的椭圆 | B. | 焦点在y轴上的椭圆 | ||
| C. | 焦点在x轴上的双曲线 | D. | 焦点在y轴上的双曲线 |
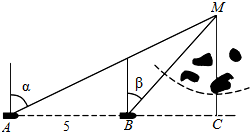 如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行.
如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行. 由曲线y=sinx,y=cosx与直线x=0,x=$\frac{π}{2}$所围成的平面图形(下图中的阴影部分)的面积是2$\sqrt{2}$-2.
由曲线y=sinx,y=cosx与直线x=0,x=$\frac{π}{2}$所围成的平面图形(下图中的阴影部分)的面积是2$\sqrt{2}$-2.