题目内容
解关于x的不等式loga(2x-1)-loga(4+3x-x2)<loga
(a>0且a≠1).
| 1 |
| 2 |
原不等式可化为
loga(4+3x-x2)>loga2(2x-1).①
当0<a<1时,①式等价于
?
,解得
,
即当0<a<1时,原不等式的解集是{x|2<x<4}.
当a>1时,①式等价于
,∴
,∴
<x<2.
即当a>1时,原不等式的解集是 {x|
<x<2}.
综上所述,当0<a<1时,原不等式的解集是{x|2<x<4};当a>1时,原不等式的解集是 {x|
<x<2}.
loga(4+3x-x2)>loga2(2x-1).①
当0<a<1时,①式等价于
|
|
|
即当0<a<1时,原不等式的解集是{x|2<x<4}.
当a>1时,①式等价于
|
|
| 1 |
| 2 |
即当a>1时,原不等式的解集是 {x|
| 1 |
| 2 |
综上所述,当0<a<1时,原不等式的解集是{x|2<x<4};当a>1时,原不等式的解集是 {x|
| 1 |
| 2 |

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
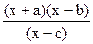 ≥0的解集为[-2,3
≥0的解集为[-2,3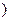 ∪[7,+∞
∪[7,+∞
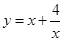
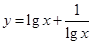
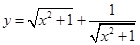

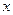 的不等式
的不等式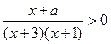 的解集是
的解集是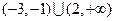 ,则
,则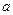 的值为_______
的值为_______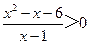 的解集为
的解集为