题目内容
已知函数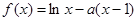 ,
,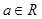 .
.
(I)讨论函数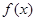 的单调性;
的单调性;
(Ⅱ)当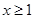 时,
时,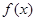 ≤
≤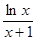 恒成立,求
恒成立,求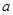 的取值范围.
的取值范围.
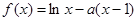 ,
,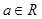 .
.(I)讨论函数
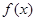 的单调性;
的单调性;(Ⅱ)当
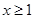 时,
时,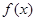 ≤
≤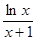 恒成立,求
恒成立,求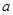 的取值范围.
的取值范围.(I)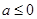 ,
,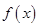 在
在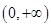 单调递增;
单调递增;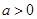 ,
,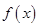 在
在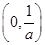 单调递增,
单调递增,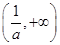 单调递减.
单调递减.
(Ⅱ)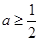 .
.
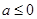 ,
,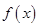 在
在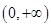 单调递增;
单调递增;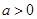 ,
,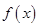 在
在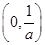 单调递增,
单调递增,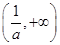 单调递减.
单调递减.(Ⅱ)
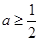 .
.试题分析:(I)根据单调函数的性质,分
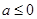 ,
,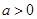 讨论
讨论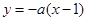 的单调性,即可得到结论.
的单调性,即可得到结论.(Ⅱ)注意到“当
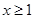 时,
时,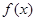 ≤
≤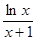 恒成立”,等价于
恒成立”,等价于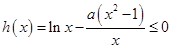 在
在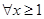 恒成立,因此,通过确定
恒成立,因此,通过确定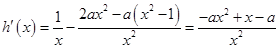 ,分以下三种情况讨论:
,分以下三种情况讨论: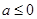 ,
,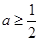 ,
,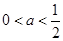 ,得出结论:
,得出结论: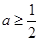 . 12分
. 12分试题解析:(I)
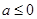 ,
,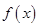 在
在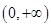 单调递增
单调递增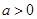 ,
,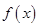 在
在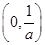 单调递增,
单调递增,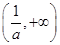 单调递减 6分
单调递减 6分(Ⅱ)等价于
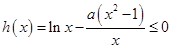 在
在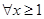 恒成立,
恒成立,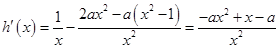
(1)当
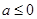 时,
时,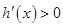 ,所以
,所以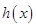 在
在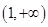 单调递增,
单调递增,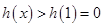 ,与题意矛盾
,与题意矛盾(2)当
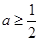 时,
时,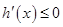 恒成立,所以
恒成立,所以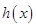 在
在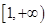 单调递减,所以
单调递减,所以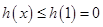
(3)当
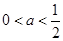 时,
时,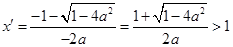 ,所以
,所以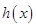 在
在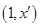 单调递增,
单调递增,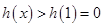 ,与题意矛盾,综上所述:
,与题意矛盾,综上所述: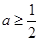 12分
12分
练习册系列答案
相关题目
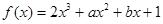 的导数为
的导数为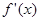 ,若函数
,若函数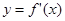 的图象关于直线
的图象关于直线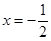 对称,且函数
对称,且函数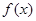 在
在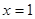 处取得极值.
处取得极值.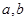 的值;
的值;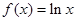 ,
,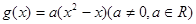 ,
,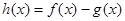
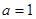 ,求函数
,求函数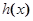 的极值;
的极值;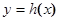 在
在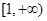 上单调递减,求实数
上单调递减,求实数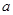 的取值范围;
的取值范围;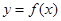 的图象上是否存在不同的两点
的图象上是否存在不同的两点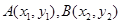 ,使线段
,使线段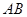 的中点的横坐标
的中点的横坐标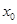 与直线
与直线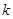 之间满足
之间满足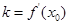 ?若存在,求出
?若存在,求出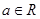 ,函数
,函数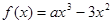 .
.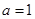 ,求函数
,求函数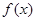 的极值与单调区间;
的极值与单调区间;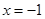 处的切线与直线
处的切线与直线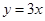 平行,求
平行,求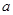 的值;
的值;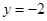 有三个公共点,求
有三个公共点,求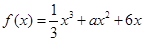 的单调递减区间是
的单调递减区间是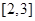 ,则实数
,则实数 .
.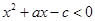 的解集为
的解集为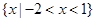 ,且函数
,且函数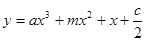 在区间
在区间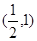 上不是单调函数,则实数
上不是单调函数,则实数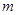 的取值范围为 ( )
的取值范围为 ( )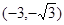
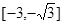
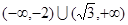
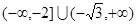
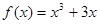 对任意的
对任意的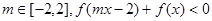 恒成立,则
恒成立,则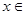 ___________.
___________.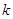 ,使得对定义域
,使得对定义域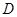 内的任意两个
内的任意两个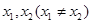 ,均有
,均有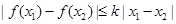 成立,则称函数
成立,则称函数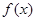 在定义域
在定义域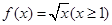 满足利普希茨条件,则常数
满足利普希茨条件,则常数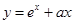 有大于零的极值点,则
有大于零的极值点,则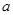 的取值范围是_________.
的取值范围是_________.