题目内容
若关于x的不等式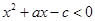 的解集为
的解集为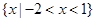 ,且函数
,且函数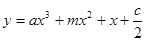 在区间
在区间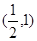 上不是单调函数,则实数
上不是单调函数,则实数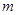 的取值范围为 ( )
的取值范围为 ( )
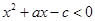 的解集为
的解集为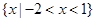 ,且函数
,且函数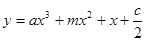 在区间
在区间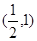 上不是单调函数,则实数
上不是单调函数,则实数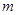 的取值范围为 ( )
的取值范围为 ( )A.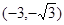 | B.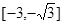 |
C.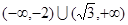 | D.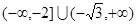 |
A
试题分析:由不等式
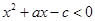 的解集为
的解集为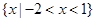 可得
可得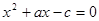 的两根为
的两根为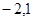 ,故可求得
,故可求得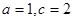 ,所以由函数
,所以由函数 在
在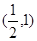 上不是单调函数,可知
上不是单调函数,可知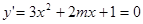 在
在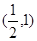 有解,当在
有解,当在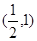 有一解时有
有一解时有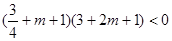 解得
解得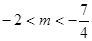 ,当在
,当在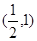 有两解时有
有两解时有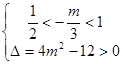 解得
解得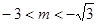 ,综上可得
,综上可得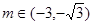 ,故选A
,故选A
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
题目内容
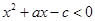 的解集为
的解集为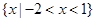 ,且函数
,且函数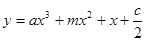 在区间
在区间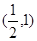 上不是单调函数,则实数
上不是单调函数,则实数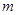 的取值范围为 ( )
的取值范围为 ( )A.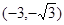 | B.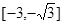 |
C.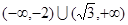 | D.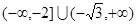 |
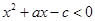 的解集为
的解集为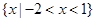 可得
可得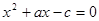 的两根为
的两根为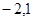 ,故可求得
,故可求得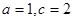 ,所以由函数
,所以由函数 在
在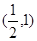 上不是单调函数,可知
上不是单调函数,可知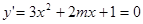 在
在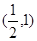 有解,当在
有解,当在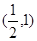 有一解时有
有一解时有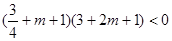 解得
解得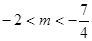 ,当在
,当在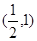 有两解时有
有两解时有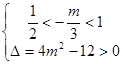 解得
解得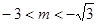 ,综上可得
,综上可得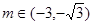 ,故选A
,故选A
 中考解读考点精练系列答案
中考解读考点精练系列答案