题目内容
【题目】如表是一个由n2个正数组成的数表，用aij表示第i行第j个数（i，j∈N），已知数表中第一列各数从上到下依次构成等差数列，每一行各数从左到右依次构成等比数列，且公比都相等．已知a11=1，a31+a61=9，a35=48． 
（1）求an1和a4n；
（2）设bn= 
+（﹣1）na 
（n∈N+），求数列{bn}的前n项和Sn ．
【答案】
（1）解：设第1列依次组成的等差公差为d，
设第1行依次组成的等比数列的公比为q，
根据题意a31+a61=（1+2d）+（1+5d）=9，
∴d=1，
∴an1=a11+（n﹣1）d=1+（n﹣1）×1=n，
∵a31=a11+2d=3，
∴a35=a31q4=3q4=48，
∵q＞0，
∴q=2，
∵a41=4，
∴a4n=a41qn﹣1=4×2n﹣1=2n+1
（2）解：由bn= 
+（﹣1）na 
（n∈N+）
= 
+（﹣1）nn
= 
+（﹣1）nn= 
﹣ 
+（﹣1）nn，
前n项和Sn=1﹣ 
+ ﹣ 
+…+ ﹣ +[﹣1+2﹣3+4﹣5+（﹣1）nn]，
当n为偶数时，Sn=1﹣ + 
；
当n为奇数时，Sn=Sn﹣1+bn=1﹣ + 
+ ﹣ ﹣n
=1﹣ ﹣ 
= 
﹣
【解析】（1）设第1列依次组成的等差公差为d，设第1行依次组成的等比数列的公比为q，根据题意可以求出d和q，再根据通项公式的定义即可求出；（2）求出bn= +（﹣1）na （n∈N+）= +（﹣1）nn= ﹣ +（﹣1）nn，根据裂项相消法和分组，讨论即可求出前n项和．
【考点精析】认真审题，首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系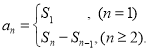
)，还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键．
