题目内容
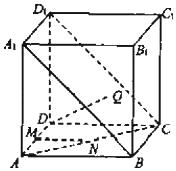
【题目】在正方体ABCD﹣A1B1C1D1中,点Q为对角面A1BCD1内一动点,点M、N分别在直线AD和AC上自由滑动,直线DQ与MN所成角的最小值为θ,则下列结论中正确的是( )
A. 若θ=15°,则点Q的轨迹为椭圆的一部分
B. 若θ=30°,则点Q的轨迹为椭圆的一部分
C. 若θ=45°,则点Q的轨迹为椭圆的一部分
D. 若θ=60°,则点Q的轨迹为椭圆的一部分
【答案】D
【解析】
先确定空间中所有满足直线DQ与MN所成角的最小值为θ的点,构成一个以D为顶点,母线与轴DD1夹角为90°﹣θ的圆锥侧面,再根据从与圆锥曲面所截的角度确定轨迹形状即可得结论.
直线DQ与MN所成角的最小值即为直线DQ与平面ABCD的夹角,
则空间中所有满足直线DQ与MN所成角的最小值为θ的点,构成一个以D为顶点,
母线与轴DD1夹角为90°﹣θ的圆锥侧面,
对角面A1BCD1与底面ABCD夹角为45°
故当θ>45°,则点Q的轨迹为椭圆的一部分
当θ=45°,则点Q的轨迹为抛物线的一部分
当0°<θ<45°,则点Q的轨迹为双曲线的一部分
故选:D.

练习册系列答案
相关题目