题目内容
19.设P(x,y)是函数y=f(x)的图象上一点,向量$\overrightarrow{a}$=(1,(x-2)5),$\overrightarrow{b}$=(1,y-2x),且满足$\overrightarrow{a}$∥$\overrightarrow{b}$,数列{an}是公差不为0的等差数列,若f(a1)+f(a2)+…+f(a9)=36,则a1+a2+…+a9=( )| A. | 0 | B. | 9 | C. | 18 | D. | 36 |
分析 由向量共线求出函数f(x)的解析式,设g(x)=f(x+2),利用函数的奇偶性以及等差数列的性质求出a5的值,从而求出a1+a2+…+a9的值.
解答 解:∵向量$\overrightarrow{a}$=(1,(x-2)5),$\overrightarrow{b}$=(1,y-2x),且$\overrightarrow{a}$∥$\overrightarrow{b}$,
∴y-2x-(x-2)5=0,
即y=(x-2)5+2x,
∴f(x)=(x-2)5+2x;
令g(x)=f(x+2)-4=x5+2x,
则函数g(x)为奇函数,且是定义域内的增函数,
由f(a1)+f(a2)+…+f(a9)=36,
得g(a1-2)+g(a2-2)+…+g(a9-2)=0,
又数列{an}是公差不为0的等差数列,
∴g(a5-2)=0,即a5-2=0,a5=2,
∴a1+a2+…+a9=9a5=9×2=18.
故选:C.
点评 本题考查了平面向量的坐标运算与等差数列的性质以及函数的性质与应用问题,是综合性问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
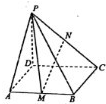 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥底面ABCD,M,N分别为AB,PC的中点,PD=AD=2,AB=4.则点A到平面PMN的距离为$\frac{\sqrt{6}}{3}$.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥底面ABCD,M,N分别为AB,PC的中点,PD=AD=2,AB=4.则点A到平面PMN的距离为$\frac{\sqrt{6}}{3}$. 用红、黄、蓝、绿、紫五种不同的颜色填充到如图所示的图形中,每格只填一种颜色,相邻两格不同色,记ξ为填充色为红色的格数,则P(ξ=2)=$\frac{6}{35}$.
用红、黄、蓝、绿、紫五种不同的颜色填充到如图所示的图形中,每格只填一种颜色,相邻两格不同色,记ξ为填充色为红色的格数,则P(ξ=2)=$\frac{6}{35}$.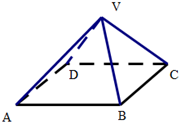 如图:正四棱锥V-ABCD中,高为2,底面ABCD是边长为4的正方形,则二面角V-AB-C的平面角为45°.
如图:正四棱锥V-ABCD中,高为2,底面ABCD是边长为4的正方形,则二面角V-AB-C的平面角为45°.