题目内容
9.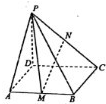 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥底面ABCD,M,N分别为AB,PC的中点,PD=AD=2,AB=4.则点A到平面PMN的距离为$\frac{\sqrt{6}}{3}$.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥底面ABCD,M,N分别为AB,PC的中点,PD=AD=2,AB=4.则点A到平面PMN的距离为$\frac{\sqrt{6}}{3}$.
分析 取PD的中点E,连接AE,NE,证明AE∥MN,可得点A到平面PMN的距离等于E到平面PMN的距离,由VE-PMN=VM-PEN,可得点A到平面PMN的距离.
解答  解:取PD的中点E,连接AE,NE,则
解:取PD的中点E,连接AE,NE,则
∵四棱锥P-ABCD中,底面ABCD是矩形,M,N分别为AB,PC的中点,
∴NE∥AM,NE=AM,
∴AENM是平行四边形,
∴AE∥MN,
∴点A到平面PMN的距离等于E到平面PMN的距离,设为h,
△PMN中,PN=$\sqrt{5}$,PM=2$\sqrt{3}$,MN=$\sqrt{5}$,∴S△PMN=$\frac{1}{2}×2\sqrt{3}×\sqrt{2}$=$\sqrt{6}$,
由VE-PMN=VM-PEN,可得$\frac{1}{3}×\sqrt{6}h=\frac{1}{3}×\frac{1}{2}×1×\frac{1}{2}×2$,
∴h=$\frac{\sqrt{6}}{3}$.
故答案为:$\frac{\sqrt{6}}{3}$.
点评 本题考查点A到平面PMN的距离,考查学生的计算能力,点A到平面PMN的距离转化为E到平面PMN的距离是关键.

练习册系列答案
相关题目
1.设函数f(x)=ax3-x+1(x∈R),若对于任意x∈[-1,1]都有f(x)≥0,则实数a的取值范围为( )
| A. | (-∞,2] | B. | [0+∞) | C. | [0,2] | D. | [1,2] |
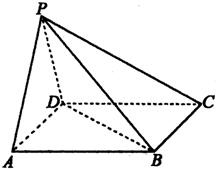 在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,平面PAD⊥底面ABCD.
在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,平面PAD⊥底面ABCD.