题目内容
11. 用红、黄、蓝、绿、紫五种不同的颜色填充到如图所示的图形中,每格只填一种颜色,相邻两格不同色,记ξ为填充色为红色的格数,则P(ξ=2)=$\frac{6}{35}$.
用红、黄、蓝、绿、紫五种不同的颜色填充到如图所示的图形中,每格只填一种颜色,相邻两格不同色,记ξ为填充色为红色的格数,则P(ξ=2)=$\frac{6}{35}$.
分析 设M表示事件“恰有两个区域用红色填充”:当区域1、4同色时,共有5×4×3×1×3=180种;当区域1、4不同色时,共有5×4×3×2×2=240种;可得所有基本事件总数为:180+240,求出1、4为红色时,2、5为红色时,即可得出.
解答 解:设M表示事件“恰有两个区域用红色填充”:
当区域1、4同色时,共有5×4×3×1×3=180种;
当区域1、4不同色时,共有5×4×3×2×2=240种;
因此,所有基本事件总数为:180+240=420种
又∵1、4为红色时,共有4×3×3=36种;
2、5为红色时,共有4×3×3=36种;
因此,事件M包含的基本事件有:36+36=72种
∴恰有两个区域用红色填充的概率P(M)=P(ξ=2)=$\frac{72}{420}$=$\frac{6}{35}$.
点评 本题考查了排列组合数的计算公式、古典概率计算公式、分类讨论思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
1.设函数f(x)=ax3-x+1(x∈R),若对于任意x∈[-1,1]都有f(x)≥0,则实数a的取值范围为( )
| A. | (-∞,2] | B. | [0+∞) | C. | [0,2] | D. | [1,2] |
16.已知命题p:“数列{an}满足an+2=3an+1-2an(n≥2)”,命题q:“数列{an+1-an}是公比为2的等比数列”,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.某学科测试中要求考生从A,B,C三道题中任选一题作答,考试结束后,统计数据显示共有600名学生参加测试,选择A,B,C三题答卷数如表:
(Ⅰ)某教师为了解参加测试的学生答卷情况,现用分层抽样的方法从600份答案中抽出若干份答卷,其中从选择A题作答的答卷中抽出了3份,则应分别从选择B,C题作答的答卷中各抽出多少份?
(Ⅱ)若在(Ⅰ)问中被抽出的答卷中,A,B,C三题答卷得优的份数都是2,从被抽出的A,B,C三题答卷中再各抽出1份,求这3份答卷中恰有1份得优的概率;
(Ⅲ)测试后的统计数据显示,B题的答卷得优的有100份,若以频率作为概率,在(Ⅰ)问中被抽出的选择B题作答的答卷中,记其中得优的份数为X,求X的分布列及其数学期望EX.
| 题 | A | B | C |
| 答卷数 | 180 | 300 | 120 |
(Ⅱ)若在(Ⅰ)问中被抽出的答卷中,A,B,C三题答卷得优的份数都是2,从被抽出的A,B,C三题答卷中再各抽出1份,求这3份答卷中恰有1份得优的概率;
(Ⅲ)测试后的统计数据显示,B题的答卷得优的有100份,若以频率作为概率,在(Ⅰ)问中被抽出的选择B题作答的答卷中,记其中得优的份数为X,求X的分布列及其数学期望EX.
 某校在一次数学考试中随机抽取了N名学生的成绩并分成一下五组,第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,已知图中从左到右后3个小组的频率之比为3:2:1,其中第4组的频数为20.
某校在一次数学考试中随机抽取了N名学生的成绩并分成一下五组,第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,已知图中从左到右后3个小组的频率之比为3:2:1,其中第4组的频数为20.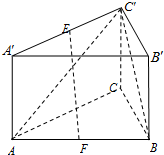 如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点.
如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点.