题目内容
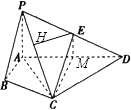
【题目】如图,在四棱锥P﹣ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,PA=2,AB=1. 
(1)设点E为PD的中点,求证:CE∥平面PAB;
(2)线段PD上是否存在一点N,使得直线CN与平面PAC所成的角θ的正弦值为 ![]() ?若存在,试确定点N的位置,若不存在,请说明理由.
?若存在,试确定点N的位置,若不存在,请说明理由.
【答案】
(1)证明:取AD中点M,连EM,CM,则EM∥PA.
∵EM平面PAB,PA平面PAB,
∴EM∥平面PAB.
在Rt△ACD中,∠CAD=60°,AC=AM=2,∴∠ACM=60°.
而∠BAC=60°,∴MC∥AB.
∵MC平面PAB,AB平面PAB,∴MC∥平面PAB.
∵EM∩MC=M,∴平面EMC∥平面PAB.
∵EC平面EMC,∴EC∥平面PAB.
(2)解:过A作AF⊥AD,交BC于F,建立如图所示的坐标系,则A(0,0,0),B( ![]() ,﹣
,﹣ ![]() ,0),C(
,0),C( ![]() ,1,0),D(0,4,0),P(0,0,2),
,1,0),D(0,4,0),P(0,0,2),
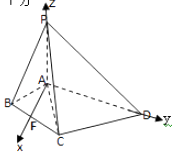
设平面PAC的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 ![]() ,取
,取 ![]() =(
=( ![]() ,﹣3,0),
,﹣3,0),
设 ![]() =λ
=λ ![]() (0≤λ≤1),则
(0≤λ≤1),则 ![]() =(0,4λ,﹣2λ),
=(0,4λ,﹣2λ), ![]() =(﹣λ﹣1,2﹣2λ),
=(﹣λ﹣1,2﹣2λ),
∴|cos< ![]() ,
, ![]() >|=
>|= ![]() =
= ![]() ,∴
,∴ ![]() ,
,
∴N为PD的中点,使得直线CN与平面PAC所成的角θ的正弦值为 ![]() .
.
【解析】(1)取AD中点M,利用三角形的中位线证明EM∥平面PAB,利用同位角相等证明MC∥AB,得到平面EMC∥平面PAB,证得EC∥平面PAB;(2)建立坐标系,求出平面PAC的法向量,利用直线CN与平面PAC所成的角θ的正弦值为 ![]() ,可得结论.
,可得结论.
【考点精析】关于本题考查的直线与平面平行的判定和空间角的异面直线所成的角,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则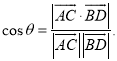 才能得出正确答案.
才能得出正确答案.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案