题目内容
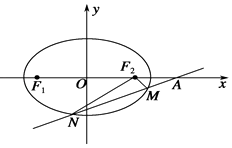
【题目】已知中心在原点的双曲线C的右焦点为(2,0),右顶点为( ![]() ,0)
,0)
(1)求双曲线C的方程;
(2)若直线l:y=kx+ ![]() 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且 ![]() >2(其中O为原点).求k的取值范围.
>2(其中O为原点).求k的取值范围.
【答案】
(1)解:设双曲线方程为 ![]() (a>0,b>0).
(a>0,b>0).
由已知得 ![]() .
.
故双曲线C的方程为 ![]() .
.
(2)解:将 ![]()
![]() .
.
由直线l与双曲线交于不同的两点得 ![]()
即 ![]() .①
.①
设A(xA,yA),B(xB,yB),
则 ![]() ,
,
而 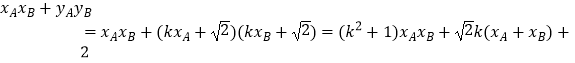 =
= ![]() .
.
于是 ![]()
![]() .②
.②
由①、②得 ![]() .
.
故k的取值范围为 ![]() .
.
【解析】(1)由双曲线的右焦点与右顶点易知其标准方程中的c、a,进而求得b,则双曲线标准方程即得;(2)首先把直线方程与双曲线方程联立方程组,然后消y得x的方程,由于直线与双曲线恒有两个不同的交点,则关于x的方程必为一元二次方程且判别式大于零,由此求出k的一个取值范围;再根据一元二次方程根与系数的关系用k的代数式表示出xA+xB , xAxB , 进而把条件 ![]() >2转化为k的不等式,又求出k的一个取值范围,最后求k的交集即可.
>2转化为k的不等式,又求出k的一个取值范围,最后求k的交集即可.

练习册系列答案
相关题目