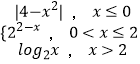题目内容
【题目】已知函数f(x)= ![]()
(1)作出函数f(x)的图象;
(2)直接写出函数f(x)的值域;
(3)求 f[f(﹣1)]的值.
【答案】
(1)解:当x≥0时,函数为y=( ![]() )x;
)x;
当x<0时,函数为y=(2)﹣x=2x,其图象由y=( ![]() )x(x≥0)和y=2x(x<0)的图象合并而成.
)x(x≥0)和y=2x(x<0)的图象合并而成.
而y=( ![]() )x(x≥0)和y=2x(x<0)的图象关于y轴对称,所以原函数图象关于y轴对称,
)x(x≥0)和y=2x(x<0)的图象关于y轴对称,所以原函数图象关于y轴对称,
图象如图:
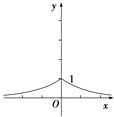
(2)解:由图象可知,值域是(0,1]
(3)解:f[f(﹣1)]=f( ![]() )=
)= ![]() =
= ![]() .
.
【解析】1、本题考查的是指数函数的图像和性质,去绝对值符号可得, 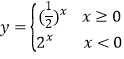 ,
,![]() 而y=(
而y=( ![]() )x(x≥0)和y=2x(x<0)的图象关于y轴对称,所以原函数图象关于y轴对称。
)x(x≥0)和y=2x(x<0)的图象关于y轴对称,所以原函数图象关于y轴对称。
2、数形结合可得。
3、本题考查的是复合函数求值的问题,由-1代入分段函数的第一个解析式得到结果再代入到第一个解析式即可。

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目