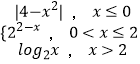Question

【题目】已知函数 ，关于x的方程f2（x）+a|f（x）|+b=0（a，b∈R）恰有6个不同实数解，则a的取值范围是 ．

Answer 1

【答案】（﹣4,﹣2）
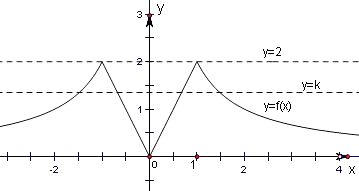
【解析】解：先根据题意作出f（x）的简图：

得f（x）＞0．

∵题中原方程f2（x）+a|f（x）|+b=0（a，b∈R）恰有6个不同实数解，即方程f2（x）+af（x）+b=0（a，b∈R）恰有6个不同实数解，

∴故由图可知，只有当f（x）=2时，它有二个根．故关于x的方程f2（x）+af（x）+b=0中，

有：4+2a+b=0，b=﹣4﹣2a，

且当f（x）=k，0＜k＜2时，关于x的方程f2（x）+af（x）+b=0有4个不同实数解，

∴k2+ak﹣4﹣2a=0，

a=﹣2﹣k，∵0＜k＜2，

∴a∈（﹣4，﹣2）．

所以答案是：（﹣4，﹣2）．