题目内容
2.解下列不等式:(1)${2^{{x^2}-5x-6}}≤1$
(2)|x-3|+|x-5|>4.
分析 (1)根据指数函数的性质,得到x2-5x-6≤0,解得即可.
(2)根据绝对值的意义|x-3|+|x-5|>4.表示数轴上的x对应点到3、5对应点的距离之和,而数轴上2和6对应点到3、5对应点的距离之和正好等于4,问题得以解决.
解答 解:(1)${2^{{x^2}-5x-6}}≤1$=20,
∴x2-5x-6≤0
∴(x+1)(x-6)≤0,
解得-1≤x≤6,
∴不等式的解集为[-1.6];
(2)根据绝对值的意义|x-3|+|x-5|>4.表示数轴上的x对应点到3、5对应点的距离之和,
而数轴上2和6对应点到3、5对应点的距离之和正好等于4,
故不等式)|x-3|+|x-5|>4的解集为{x|x<2,或x>6}
点评 本题主要考查绝对值的意义,绝对值不等式的解法,属于中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
13.抛掷质地均匀的甲、乙两颗骰子,设出现的点数分别为a、b,则满足$\frac{a}{2}$<|b-a2|<6-a的概率为( )
| A. | $\frac{13}{36}$ | B. | $\frac{5}{18}$ | C. | $\frac{7}{36}$ | D. | $\frac{5}{36}$ |
17.已知数列{an}是等差数列,且a6+a7=10,则在(x-a1)(x-a2)…(x-a12)的展开式中,x11项的系数是( )
| A. | 60 | B. | -60 | C. | 30 | D. | -30 |
7.f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(-3)=0,则不等式f(x)g(x)<0的解集是( )
| A. | (-∞,-3)∪(0,3) | B. | (-∞,-3)∪(3,+∞) | C. | (-3,0)∪(3,+∞) | D. | (-3,0)∪(0,3) |
12.设集合A={1,2,3},B={2,3,4},C⊆A∩B,则集合C可能是( )
| A. | {1,2} | B. | {1,3} | C. | {2,3} | D. | {2,4} |
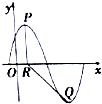 已知函数f(x)=Asin($\frac{π}{3}x$+φ),(A>0,0<φ<$\frac{π}{2}$),y=f(x)的部分图象如图所示,P,Q分别为该图象上相邻的最高点和最低点,点P在x轴上的射影为R(1,0),cos∠PRQ=-$\frac{4}{5}$.
已知函数f(x)=Asin($\frac{π}{3}x$+φ),(A>0,0<φ<$\frac{π}{2}$),y=f(x)的部分图象如图所示,P,Q分别为该图象上相邻的最高点和最低点,点P在x轴上的射影为R(1,0),cos∠PRQ=-$\frac{4}{5}$.