题目内容
20.证明:(1)$\frac{x}{x+1}$≤ln(x+1)≤x;
(2)ex≥x+1.
分析 (1)令f(x)=(x+1)ln(x+1)-x,结合函数的单调性,分类讨论,即可证明;令g(x)=x-ln(x+1),根据它的导数的符号可得函数g(x)的单调性,再根据函数的单调性求得函数g(x)取得最小值为0,即g(x)≥0,从而证得不等式.
(2)首先构造函数f(x)=ex-x-1,然后求出函数的导数,利用导数与函数单调性的关系进行证明.
解答 证明:(1)令f(x)=(x+1)ln(x+1)-x,
则f′(x)=ln(x+1)+1-1=ln(x+1),
-1<x<0,f′(x)<0,
∴f(x)在-1<x<0时单调递减,
∴(x+1)ln(x+1)-x<0成立,
∴$\frac{x}{x+1}$≤ln(x+1);
x=0,等号成立;
x>0,∴ln(x+1)>ln1=0,
即f′(x)>0,
∴f(x)在x>0时单调递增,
∴f(x)>f(0)=0
∴(x+1)ln(x+1)-x>0成立,
∴$\frac{x}{x+1}$≤ln(x+1).
令g(x)=x-ln(x+1),则它的导数为 g′(x)=1-$\frac{1}{x+1}$.
当0>x>-1时,g′(x)<0,故函数g(x)在(-1,0)上是减函数.
当x≥0时,g′(x)≥0,当且仅当x=0时,g′(x)=0,故函数g(x)在[0,+∞)上是增函数.
故当x=0时,函数g(x)取得最小值为0,
故有g(x)=x-ln(x+1)≥0,∴ln(x+1)≤x.
∴$\frac{x}{x+1}$≤ln(x+1)≤x;
(2)设f(x)=ex-x-1,则f′(x)=ex-1,
∴当x=0时,f′(x)=0,f(x)=0.
当x>0时,f′(x)>0,
∴f(x)在(0,+∞)上是增函数,
∴f(x)>f(0)=0.
当x<0时,f′(x)<0,
∴f(x)在(-∞,0)上是减函数,
∴f(x)>f(0)=0.
∴对x∈R都有f(x)≥0,
∴ex≥x+1.
点评 本题主要考查函数导数与函数单调性之间的关系,根据函数的单调性求函数的最值,体现了转化的数学思想,掌握并会熟练运用导数与函数单调性的关系是关键,属于中档题.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案| A. | 第一象限内点的集合 | B. | 第三象限内点的集合 | ||
| C. | 第一、三象限内点的集合 | D. | 第二、四象限内点的集合 |
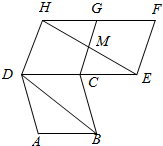 如图,四边形ABCD,CEFG,CGFD都是全等的菱形,HE与CG相交于点M,则下列关系不一定成立的是( )
如图,四边形ABCD,CEFG,CGFD都是全等的菱形,HE与CG相交于点M,则下列关系不一定成立的是( )| A. | |$\overrightarrow{AB}$|=|$\overrightarrow{EF}$| | B. | $\overrightarrow{AB}$与$\overrightarrow{FH}$共线 | C. | $\overrightarrow{BD}$与$\overrightarrow{EH}$共线 | D. | $\overrightarrow{DC}$与$\overrightarrow{EC}$共线 |
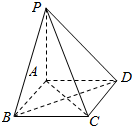 如图,四棱锥P-ABCD中,PA⊥平面ABCD,ABCD为正方形,则该四棱锥中互相垂直的平面有6组.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,ABCD为正方形,则该四棱锥中互相垂直的平面有6组.