题目内容
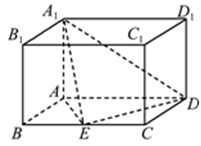
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥平面ABC,△ABC为正三角形,且侧面AA1C1C是边长为2的正方形,E是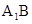 的中点,F在棱CC1上。
的中点,F在棱CC1上。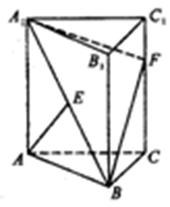
(1)当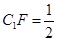 CF时,求多面体ABCFA1的体积;
CF时,求多面体ABCFA1的体积;
(2)当点F使得A1F+BF最小时,判断直线AE与A1F是否垂直,并证明的结论。
(1) 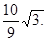 ;(2)
;(2) 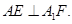 ,证明详见解析
,证明详见解析
解析试题分析:(1)此多面体是以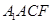 为底面,以B为顶点的四棱锥,而且
为底面,以B为顶点的四棱锥,而且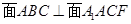 ,因为△ABC为正三角形,所以△ABC的AC边上的高即为此四棱锥的高,底面
,因为△ABC为正三角形,所以△ABC的AC边上的高即为此四棱锥的高,底面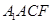 是直角梯形,所以利用锥体体积公式即可求得其体积。(2)把立体图展成平面图后,两点之间直线最短,连接
是直角梯形,所以利用锥体体积公式即可求得其体积。(2)把立体图展成平面图后,两点之间直线最短,连接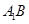 交
交 与点F,此时A1F+BF最小,分析可知F为
与点F,此时A1F+BF最小,分析可知F为 的中点。过点
的中点。过点 作
作 交
交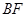 于
于 ,则
,则 是
是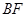 的中点,此时只需判断AE与EG是否垂直即可。求出三角形AEG三边长即可得证,详见解析。
的中点,此时只需判断AE与EG是否垂直即可。求出三角形AEG三边长即可得证,详见解析。
试题解析:解:(Ⅰ)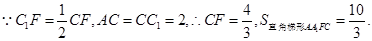
由已知可得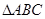 的高为
的高为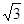 且等于四棱锥
且等于四棱锥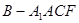 的高.
的高.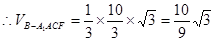 ,即多面体
,即多面体 的体积为
的体积为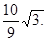 5分
5分
(Ⅱ)将侧面 展开到侧面
展开到侧面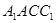 得到矩形
得到矩形 ,连结
,连结 ,交
,交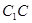 于点
于点 ,此时点
,此时点 使得
使得 最小.此时
最小.此时 平行且等于
平行且等于 的一半,
的一半,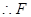 为
为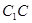 的中点. 7分
的中点. 7分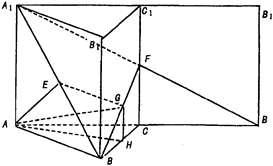
过点 作
作 交
交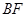 于
于 ,则
,则 是
是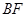 的中点,
的中点,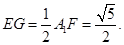 .
.
过点 作
作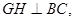 交
交 于
于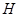 ,则
,则
又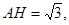 于是在
于是在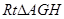 中,
中, 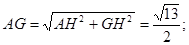
在 中,
中,
在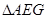 中,
中,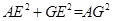 ,
, ∴
∴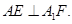 13分
13分
考点:几何体体积,线线垂直。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

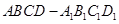 中,
中,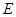 为线段
为线段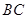 的中点,
的中点,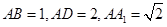 .
.
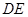 ⊥平面
⊥平面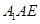 ;
;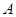 到平面
到平面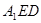 的距离.
的距离. 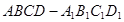 中,
中,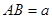 ,
,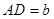 ,
,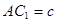 ,点
,点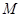 为
为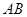 的中点,点
的中点,点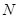 为
为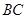 的中点.
的中点.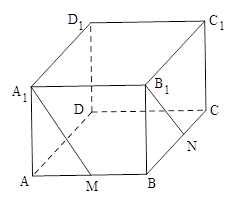
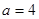 ,
,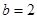 ,
,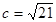 ,求异面直线
,求异面直线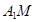 与
与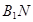 所成的角.
所成的角. 的球内有一个内接正方体(即正方体的顶点都在球面上).
的球内有一个内接正方体(即正方体的顶点都在球面上). 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.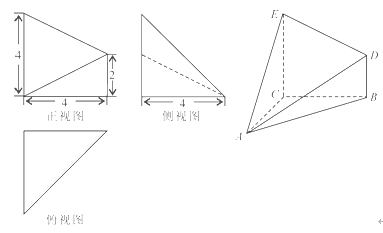
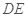 与
与 所成角的余弦值;
所成角的余弦值;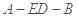 的正弦值;
的正弦值; 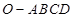 中,底面
中,底面 是边长为
是边长为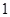 的菱形,
的菱形,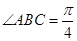 ,
, 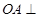 底面
底面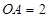 ,
,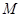 为
为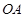 的中点,
的中点,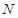 为
为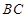 的中点.
的中点.
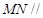 平面
平面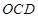 .
. 与
与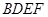 均为菱形,设
均为菱形,设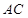 与
与 相交于点
相交于点 ,若
,若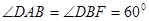 ,且
,且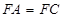 .
.
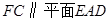 ;
;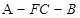 的余弦值.
的余弦值. 的底面为直角梯形,
的底面为直角梯形,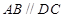 ,
,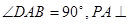 底面
底面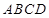 ,且
,且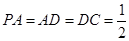 ,
,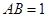 ,
,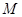 是
是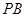 的中点。
的中点。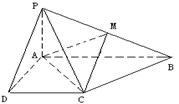
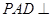 面
面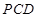 ;
;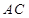 与
与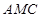 与面
与面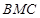 所成二面角的大小。
所成二面角的大小。