题目内容
已知半径为 的球内有一个内接正方体(即正方体的顶点都在球面上).
的球内有一个内接正方体(即正方体的顶点都在球面上).
(1)求此球的体积;
(2)求此球的内接正方体的体积;
(3)求此球的表面积与其内接正方体的全面积之比.
(1)V=4
 ;(2)V=8;(3)球的表面积与其内接正方体的全面积之比为
;(2)V=8;(3)球的表面积与其内接正方体的全面积之比为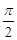 .
.
解析试题分析:(1)球的体积公式为V=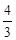
 R3,将R=
R3,将R= 代入可得V=4
代入可得V=4
 ;(2)要求内接正方体的体积,需要知道正方体的棱长,正方体的对角线是球的直径,而正方体的对角线是棱长的
;(2)要求内接正方体的体积,需要知道正方体的棱长,正方体的对角线是球的直径,而正方体的对角线是棱长的 倍,设正方体的棱长为a,所以2
倍,设正方体的棱长为a,所以2 =
= a,a="2," V=a3=8;(3)求出正方体的表面积和球的表面积,从而得出球的球面面积与其内接正方体的全面积之比,S球=4
a,a="2," V=a3=8;(3)求出正方体的表面积和球的表面积,从而得出球的球面面积与其内接正方体的全面积之比,S球=4 R2=12
R2=12 ,S正方体=6a2=24,所以这个球的表面积与其内接正方体的全面积之比为12
,S正方体=6a2=24,所以这个球的表面积与其内接正方体的全面积之比为12 :24=
:24=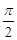 .
.
试题解析:(1)球的体积V=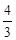
 R3=4
R3=4
 ;
;
(2)设正方体的棱长为a,
∴2 =
=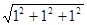 a =
a = a,a="2," V=a3=8;
a,a="2," V=a3=8;
(3)S球=4 R2=12
R2=12 ,
,
S正方体=6a2=24,
∴这个球的表面积与其内接正方体的全面积之比为12 :24=
:24=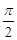 .
.
考点:1.球的体积公式;2.球内接多面体.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
 中,
中, ,
,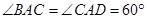 ,
, ,
,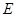 为
为 的中点,
的中点,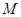 为
为 的中点,
的中点, .
.
 ;
;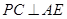 ;
; 的体积
的体积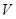 .
.
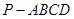 中,底面
中,底面 是边长为1的正方形,
是边长为1的正方形,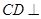 平面
平面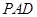 ,
, 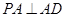 ,
,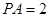 ,
,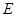 为
为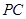 的中点,
的中点,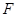 在棱
在棱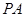 上.
上.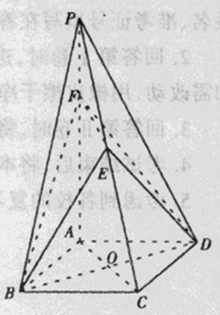
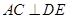 ;
;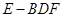 的体积.
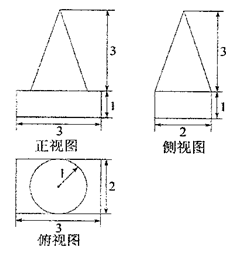
的体积. 的三视图和直观图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图和直观图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形. 是侧棱
是侧棱 上的动点.
上的动点.

 ;
; 与平面
与平面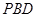 所成角的正弦值.
所成角的正弦值.  的中点,F在棱CC1上。
的中点,F在棱CC1上。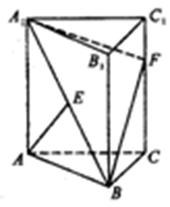
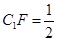 CF时,求多面体ABCFA1的体积;
CF时,求多面体ABCFA1的体积; ),
),
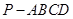 的底面是正方形,
的底面是正方形,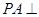 底面
底面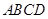 ,
,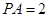 ,
, ,点
,点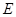 、
、 分别为棱
分别为棱 、
、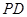 的中点.
的中点.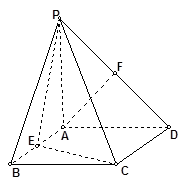
 平面
平面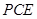 ;
;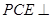 平面
平面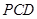 ;
;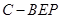 的体积.
的体积.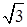 ,AD=CD=1.
,AD=CD=1.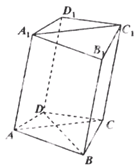
 求证:BD⊥AA1;
求证:BD⊥AA1; 若四边形
若四边形 是菱形,且
是菱形,且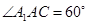 ,求四棱柱
,求四棱柱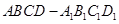 的体积.
的体积.