题目内容
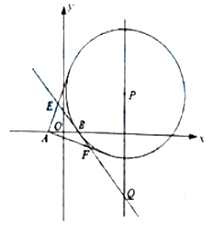
【题目】如图，已知椭圆C： 
+ 
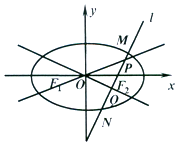
=1（a＞b＞0）的左、右焦点分别为F1、F2 ， 焦距为2，过点F2作直线l交椭圆于M、N两点，△F1MN的周长为8． 
（Ⅰ）求椭圆C的方程；
（Ⅱ）若直线l分别交直线y= 
x，y=﹣ x于P，Q两点，求 
的取值范围．
【答案】解：（Ⅰ）∵椭圆C： 
+ 
=1（a＞b＞0）的左、右焦点分别为F1、F2，焦距为2，
过点F2作直线l交椭圆于M、N两点，△F1MN的周长为8．
∴ 
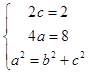，解得a=2，b= 
，c=1，
∴椭圆方程为 
．
（Ⅱ）设直线l的方程为x=my+1，
联立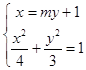 
，消去x，整理，得：（3m2+4）y2+6my﹣9=0，
设M（x1，y1），N（x2，y2），则 
， 
，
设P（x3，y3），N（x4，y4），
联立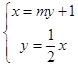 
，得 
，同理 
，
|PQ|= 
= 
，
∴ 
= 
= 
，
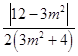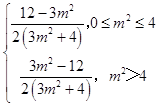当0≤m2≤4时， = 
∈[0， 
]，
当m2＞4时， = 
∈（0， 
），
∴ 的取值范围是[0， ]．
【解析】（Ⅰ）由椭圆的焦距为2，过点F2作直线l交椭圆于M、N两点，△F1MN的周长为8，列出方程组求出a，b，由此能求出椭圆方程．（Ⅱ）设直线l的方程为x=my+1，联立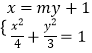 
，得：（3m2+4）y2+6my﹣9=0，由此利用韦达定理、弦长公式、三角形面积公式，结合已知条件能求出 
的取值范围．
【考点精析】本题主要考查了椭圆的标准方程的相关知识点，需要掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
才能正确解答此题．
练习册系列答案
相关题目
