题目内容
【题目】在极坐标系下,已知圆O:ρ=cosθ+sinθ和直线l:![]() .
.
(1)求圆O和直线l的直角坐标方程;
(2)当θ∈(0,π)时,求直线l与圆O公共点的极坐标.
【答案】(1)x﹣y+1=0.(2)![]()
【解析】
试题(1)圆O的方程即ρ2=ρcosθ+ρsinθ,可得圆O 的直角坐标方程为:x2+y2=x+y,即x2+y2﹣x﹣y=0.
(2)由![]() ,可得直线l与圆O公共点的直角坐标为(0,1),由此求得线l与圆O公共点的极坐标.
,可得直线l与圆O公共点的直角坐标为(0,1),由此求得线l与圆O公共点的极坐标.
解:(1)圆O:ρ=cosθ+sinθ,即ρ2=ρcosθ+ρsinθ,
故圆O 的直角坐标方程为:x2+y2=x+y,即x2+y2﹣x﹣y=0.
直线l:![]() ,即ρsinθ﹣ρcosθ=1,则直线的直角坐标方程为:y﹣x=1,即x﹣y+1=0.
,即ρsinθ﹣ρcosθ=1,则直线的直角坐标方程为:y﹣x=1,即x﹣y+1=0.
(2)由![]() ,可得
,可得![]() ,直线l与圆O公共点的直角坐标为(0,1),
,直线l与圆O公共点的直角坐标为(0,1),
故直线l 与圆O 公共点的一个极坐标为![]() .
.

练习册系列答案
相关题目
【题目】为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
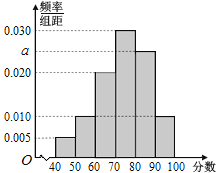
(1)求![]() 的值;
的值;
(2)估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(3)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99.9%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |